
【題目】如圖,已知矩形![]() 所在平面垂直于直角梯形
所在平面垂直于直角梯形![]() 所在平面,平面
所在平面,平面![]() 平面
平面![]() ,且
,且![]() ,且
,且![]() .
.

(1)設(shè)點![]() 為棱
為棱![]() 中點,在面
中點,在面![]() 內(nèi)是否存在點
內(nèi)是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,請證明,若不存在,說明理由;
?若存在,請證明,若不存在,說明理由;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)存在點![]() ,為
,為![]() 中點;(2)
中點;(2)![]()
【解析】
試題分析:(1)由題意可知![]() 平面
平面![]() ,所以只要構(gòu)造直線
,所以只要構(gòu)造直線![]() 即可,連接
即可,連接![]() ,取
,取![]() 中點
中點![]() ,構(gòu)造三角形
,構(gòu)造三角形![]() 的中位線即可;(2)以A為原點,AE,AB,AD所在直線分別為
的中位線即可;(2)以A為原點,AE,AB,AD所在直線分別為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建立坐標(biāo)系,求出平面
軸建立坐標(biāo)系,求出平面![]() 與平面
與平面![]() 的法向量,利用空間向量相關(guān)知識求解即可.
的法向量,利用空間向量相關(guān)知識求解即可.
試題解析:(1)連接![]() ,
,![]() 交于點
交于點![]() ,連接
,連接![]() ,則
,則![]() 平面
平面![]()
證明:![]()
![]() 為
為![]() 中點,
中點,![]() 為
為![]() 中點
中點
![]() 為
為![]() 的中位線,
的中位線,![]()
又平面![]() 平面
平面![]()
平面![]()
![]() 平面
平面![]() =
=![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]()
![]() ,
,
又![]() ,
,![]()
![]() 平面
平面![]()
所以![]() 平面
平面![]()
(2)以A為原點,AE,AB,AD所在直線分別為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建立坐標(biāo)系,
軸建立坐標(biāo)系,
![]() 平面PEA
平面PEA
![]() 平面PEA的法向量
平面PEA的法向量![]()
另外![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,設(shè)平面DPE的法向量
,設(shè)平面DPE的法向量![]() ,則
,則
![]() ,令
,令![]() ,得
,得![]()
![]()
又![]() 為銳二面角,所以二面角
為銳二面角,所以二面角![]() 的余弦值為
的余弦值為![]()


 暑假銜接教材期末暑假預(yù)習(xí)武漢出版社系列答案
暑假銜接教材期末暑假預(yù)習(xí)武漢出版社系列答案 假期作業(yè)暑假成長樂園新疆青少年出版社系列答案
假期作業(yè)暑假成長樂園新疆青少年出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】從3名男生和2名女生中任選兩人參加演講比賽,試求:
(1)所選2人都是男生的概率;
(2)所選2人恰有1名女生的概率;
(3)所選2人至少有1名女生的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在某海濱城市附近海面有一臺風(fēng),據(jù)監(jiān)測,當(dāng)前臺風(fēng)中心位于城市![]() (如圖)的東偏南
(如圖)的東偏南![]() 方向300km的海面
方向300km的海面![]() 處,并以20km/h的速度向西偏北
處,并以20km/h的速度向西偏北![]() 方向移動,臺風(fēng)侵襲的范圍為圓形區(qū)域,當(dāng)前半徑為60km,并以10km/h的速度不斷增大,問幾小時后該城市開始受到臺風(fēng)的侵襲?受到臺風(fēng)侵襲的時間有多少小時?
方向移動,臺風(fēng)侵襲的范圍為圓形區(qū)域,當(dāng)前半徑為60km,并以10km/h的速度不斷增大,問幾小時后該城市開始受到臺風(fēng)的侵襲?受到臺風(fēng)侵襲的時間有多少小時?
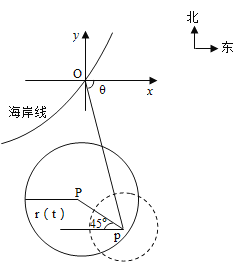
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知集合A,B,若A不是B的子集,則下列命題中正確的是( )
A.對任意的a∈A,都有aB
B.對任意的b∈B,都有bA
C.存在a0 , 滿足a0∈A,a0B
D.存在a0 , 滿足a0∈A,a0∈B
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分12分)某旅行社設(shè)計了一個組織旅游團(tuán)包飛機(jī)去廣州旅游的方案,其中旅行杜的包機(jī)費用為![]() 元,旅游團(tuán)中最多能有
元,旅游團(tuán)中最多能有![]() 人,并且旅游團(tuán)中的人數(shù)
人,并且旅游團(tuán)中的人數(shù)![]() (單位:個)與每個人交給旅行社的費用
(單位:個)與每個人交給旅行社的費用![]() (單位:元)的關(guān)系如下:
(單位:元)的關(guān)系如下: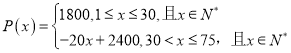 .
.
(1)將旅行社的利潤![]() (單位:元)表示成旅游團(tuán)中的人數(shù)
(單位:元)表示成旅游團(tuán)中的人數(shù)![]() 的函數(shù)(注:利潤=收取的費用一包機(jī)費用);
的函數(shù)(注:利潤=收取的費用一包機(jī)費用);
(2)當(dāng)旅游團(tuán)有多少人時,旅行社的利潤最大?并求出最大利潤.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c,已知cos C+(cos A-![]() sin A)cos B=0.
sin A)cos B=0.
(1)求角B的大小;
(2)若a+c=1,求b的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知等差數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,并且
,并且![]() ,數(shù)列
,數(shù)列![]() 滿足:
滿足:![]() ,記數(shù)列
,記數(shù)列![]() 的前
的前![]() 項和為
項和為![]() .
.
(1)求數(shù)列![]() 的通項公式
的通項公式![]() 及前
及前![]() 項和為
項和為![]() ;
;
(2)求數(shù)列![]() 的通項公式
的通項公式![]() 及前
及前![]() 項和為
項和為![]() ;
;
(3)記集合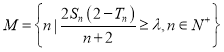 ,若
,若![]() 的子集個數(shù)為16,求實數(shù)
的子集個數(shù)為16,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com