Question

某電視臺組織部分記者，用“10分制”隨機調查某社區居民的幸福指數.現從調查人群中隨機抽取16名，如圖所示的莖葉圖記錄了他們的幸福指數的得分(以小數點前的一位數字為莖，小數點后的一位數字為葉)：

（1）指出這組數據的眾數和中位數；
（2）若幸福指數不低于9.5分，則稱該人的幸福指數為“極幸福”.求從這16人中隨機選取3人，至多有1人是“極幸福”的概率；
（3）以這16人的樣本數據來估計整個社區的總體數據，若從該社區(人數很多)任選3人，記表示抽到“極幸福”的人數，求的分布列及數學期望．

Answer 1

（1）8.6,8.75；（2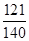）；（3）參考解析

解析試題分析：（1）由眾數即為樣本中出現次數最多的數字，中位數即為樣本數據從小到大排序最中間的那個數字或是最中間的兩個數字.根據所給的數字即可得到結論.
（2）因為幸福指數不低于9.5分的共有4人，求從這16人中隨機選取3人，至多有1人是“極幸福”的概率，轉化為16人中一人是“極幸福”的概率加上沒有人是“極幸福”的概率.通過計算即可得到所求的結論.
（3）若從該社區(人數很多)任選3人，記表示抽到“極幸福”的人數，共有四種情況，并且分別求出各種情況的概率，從而得到數學期望值.
試題解析：（1）眾數：8.6；中位數：8.75 ；
（2）設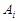表示所取3人中有個人是“極幸福”，至多有1人是“極幸福”記為事件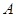， 則 ；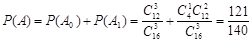
（3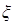）的可能取值為0，1，2，3.
；；
；.
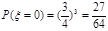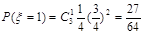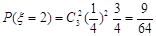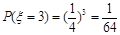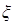的分布列為：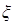

.
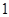
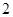
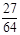
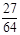
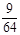
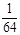
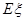
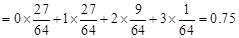另解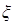：的可能取值為0，1，2，3,則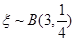，因此.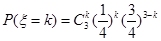
有；；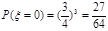
；.
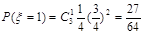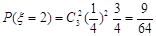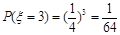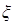的分布列為：