
【題目】在直角坐標(biāo)系![]() 中,已知
中,已知![]() ,
,![]() 為拋物線(xiàn)
為拋物線(xiàn)![]() :
:![]() 上兩點(diǎn),
上兩點(diǎn),![]() 為拋物線(xiàn)焦點(diǎn).分別過(guò)
為拋物線(xiàn)焦點(diǎn).分別過(guò)![]() ,
,![]() 作拋物線(xiàn)的切線(xiàn)交于點(diǎn)
作拋物線(xiàn)的切線(xiàn)交于點(diǎn)![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,
,![]() 分別交
分別交![]() 軸于
軸于![]() ,
,![]() 兩點(diǎn),試問(wèn)
兩點(diǎn),試問(wèn)![]() 的外接圓是否過(guò)定點(diǎn)?若是,求出該定點(diǎn)坐標(biāo),若不是,請(qǐng)說(shuō)明理由.
的外接圓是否過(guò)定點(diǎn)?若是,求出該定點(diǎn)坐標(biāo),若不是,請(qǐng)說(shuō)明理由.
【答案】(1)![]() ;(2)見(jiàn)解析
;(2)見(jiàn)解析
【解析】
(1)設(shè)直線(xiàn)![]() 的方程為
的方程為![]() ,與拋物線(xiàn)聯(lián)立可得
,與拋物線(xiàn)聯(lián)立可得![]() ,由
,由![]() 可得
可得![]() ,可解出
,可解出![]() 的值,然后由
的值,然后由![]() 可得到答案;(2)設(shè)
可得到答案;(2)設(shè)![]() ,可表示出直線(xiàn)
,可表示出直線(xiàn)![]() 的方程
的方程![]() ,令
,令![]() ,可得
,可得![]() ,然后可以證明
,然后可以證明![]() ,即
,即![]() ,同理可證明
,同理可證明![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() 四點(diǎn)共圓,即
四點(diǎn)共圓,即![]() 的外接圓過(guò)定點(diǎn)
的外接圓過(guò)定點(diǎn)![]() .
.
(1)由題意知直線(xiàn)![]() 的斜率存在,設(shè)其為
的斜率存在,設(shè)其為![]() ,
,
則![]() .
.
設(shè)![]() ,
,![]() ,則由根與系數(shù)關(guān)系有
,則由根與系數(shù)關(guān)系有![]() ①
①
由![]() 可得
可得![]() ②
②
結(jié)合①②可求得![]() .
.
所以![]() .
.
(2)![]() 的外接圓過(guò)定點(diǎn)
的外接圓過(guò)定點(diǎn)![]() ,
,
拋物線(xiàn)方程為![]() ,求導(dǎo)得
,求導(dǎo)得![]() ,設(shè)
,設(shè)![]() ,
,
可知直線(xiàn)![]() 方程
方程![]() ,
,
令![]() ,得
,得![]() ,故
,故![]() ,
,![]() .
.
所以![]() .
.
同理可得![]() .
.
故![]() ,
,![]() ,
,![]() ,
,![]() 四點(diǎn)共圓,即
四點(diǎn)共圓,即![]() 的外接圓過(guò)定點(diǎn)
的外接圓過(guò)定點(diǎn)![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列說(shuō)法中,正確的命題是( )
A.已知隨機(jī)變量![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,
,![]() ,則
,則![]()
B.由獨(dú)立性檢驗(yàn)可知,有99%的把握認(rèn)為物理成績(jī)與數(shù)學(xué)成績(jī)有關(guān),某人數(shù)學(xué)成績(jī)優(yōu)秀,則他有99%的可能物理優(yōu)秀
C.以模型![]() 去擬合一組數(shù)據(jù)時(shí),為了求出回歸方程,設(shè)
去擬合一組數(shù)據(jù)時(shí),為了求出回歸方程,設(shè)![]() ,將其變換后得到線(xiàn)性方程
,將其變換后得到線(xiàn)性方程![]() ,則c,k的值分別是
,則c,k的值分別是![]() 和0.3
和0.3
D.在回歸分析模型中,殘差平方和越大,說(shuō)明模型的擬合效果越差
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某地區(qū)2020年清明節(jié)前后3天每天下雨的概率為70%,通過(guò)模擬實(shí)驗(yàn)的方法來(lái)計(jì)算該地區(qū)這3天中恰好有2天下雨的概率:用隨機(jī)數(shù)![]() (
(![]() ,且
,且![]() )表示是否下雨:當(dāng)
)表示是否下雨:當(dāng)![]() 時(shí)表示該地區(qū)下雨,當(dāng)
時(shí)表示該地區(qū)下雨,當(dāng)![]() 時(shí),表示該地區(qū)不下雨,從隨機(jī)數(shù)表中隨機(jī)取得20組數(shù)如下:
時(shí),表示該地區(qū)不下雨,從隨機(jī)數(shù)表中隨機(jī)取得20組數(shù)如下:
332 714 740 945 593 468 491 272 073 445
992 772 951 431 169 332 435 027 898 719
(1)求出![]() 的值,并根據(jù)上述數(shù)表求出該地區(qū)清明節(jié)前后3天中恰好有2天下雨的概率;
的值,并根據(jù)上述數(shù)表求出該地區(qū)清明節(jié)前后3天中恰好有2天下雨的概率;
(2)從2011年開(kāi)始到2019年該地區(qū)清明節(jié)當(dāng)天降雨量(單位:![]() )如下表:(其中降雨量為0表示沒(méi)有下雨).
)如下表:(其中降雨量為0表示沒(méi)有下雨).
時(shí)間 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
降雨量 | 29 | 28 | 26 | 27 | 25 | 23 | 24 | 22 | 21 |
經(jīng)研究表明:從2011年開(kāi)始至2020年, 該地區(qū)清明節(jié)有降雨的年份的降雨量![]() 與年份
與年份![]() 成線(xiàn)性回歸,求回歸直線(xiàn)
成線(xiàn)性回歸,求回歸直線(xiàn)![]() ,并計(jì)算如果該地區(qū)2020年(
,并計(jì)算如果該地區(qū)2020年(![]() )清明節(jié)有降雨的話(huà),降雨量為多少?(精確到0.01)
)清明節(jié)有降雨的話(huà),降雨量為多少?(精確到0.01)
參考公式: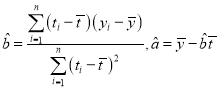 .
.
參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】我國(guó)南宋數(shù)學(xué)家楊輝1261年所著的《詳解九章算法》一書(shū)里出現(xiàn)了如圖所示的表,即楊輝三角,這是數(shù)學(xué)史上的一個(gè)偉大成就.在“楊輝三角”中,第![]() 行的所有數(shù)字之和為
行的所有數(shù)字之和為![]() ,若去除所有為1的項(xiàng),依次構(gòu)成數(shù)列
,若去除所有為1的項(xiàng),依次構(gòu)成數(shù)列![]() ,則此數(shù)列的前55項(xiàng)和為( )
,則此數(shù)列的前55項(xiàng)和為( )

A. 4072B. 2026C. 4096D. 2048
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在正方形ABCD的一邊CD內(nèi)任取一點(diǎn)E,過(guò)E作對(duì)角線(xiàn)AC的平行線(xiàn),交對(duì)角線(xiàn)BD于點(diǎn)G、交邊AD于點(diǎn)H、交邊BA的延長(zhǎng)線(xiàn)于點(diǎn)F,聯(lián)結(jié)BH交DF于點(diǎn)M.求證:
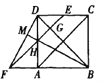
(1)C、G、M三點(diǎn)共線(xiàn);
(2)C、E、M、F四點(diǎn)共圓.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
,![]()
(1)當(dāng)![]() 時(shí),求
時(shí),求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)當(dāng)![]() ,討論
,討論![]() 的零點(diǎn)個(gè)數(shù);
的零點(diǎn)個(gè)數(shù);
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為推動(dòng)乒乓球運(yùn)動(dòng)的發(fā)展,某乒乓球比賽允許不同協(xié)會(huì)的運(yùn)動(dòng)員組隊(duì)參加.現(xiàn)有來(lái)自甲協(xié)會(huì)的運(yùn)動(dòng)員3名,其中種子選手2名;乙協(xié)會(huì)的運(yùn)動(dòng)員5名,其中種子選手3名.從這8名運(yùn)動(dòng)員中隨機(jī)選擇4人參加比賽.
(1)設(shè)A為事件“選出的4人中恰有2名種子選手,且這2名種子選手來(lái)自同一個(gè)協(xié)會(huì)”,求事件![]() 發(fā)生的概率;
發(fā)生的概率;
(2)設(shè)![]() 為選出的4人中種子選手的人數(shù),求隨機(jī)變量
為選出的4人中種子選手的人數(shù),求隨機(jī)變量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某縣共有90間農(nóng)村淘寶服務(wù)站,隨機(jī)抽取5間,統(tǒng)計(jì)元旦期間的網(wǎng)購(gòu)金額(單位:萬(wàn)元)的莖葉圖如圖所示,其中莖為十位數(shù),葉為個(gè)位數(shù).若網(wǎng)購(gòu)金額(單位:萬(wàn)元)不小于18的服務(wù)站定義為優(yōu)秀服務(wù)站,其余為非優(yōu)秀服務(wù)站.從隨機(jī)抽取的5間服務(wù)站中再任取2間作網(wǎng)購(gòu)商品的調(diào)查,則恰有1間是優(yōu)秀服務(wù)站的概率為_____.
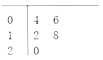
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com