Question

【題目】如圖所示，某小區準備將閑置的一直角三角形(其中∠B＝，AB＝a，BC＝a)地塊開發成公共綠地，設計時，要求綠地部分有公共綠地走道MN，且兩邊是兩個關于走道MN對稱的三角形(△AMN和△A′MN)，現考慮方便和綠地最大化原則，要求M點與B點不重合，A′落在邊BC上，設∠AMN＝θ.

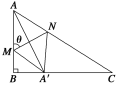
(1)若θ＝時，綠地“最美”，求最美綠地的面積；

(2)為方便小區居民的行走，設計時要求將AN，A′N的值設計最短，求此時綠地公共走道的長度.

Answer 1

【答案】見解析

【解析】解 (1)由∠B＝，AB＝a，BC＝a，

所以∠BAC＝.

設MA＝MA′＝xa(0<x<1)，則MB＝a－xa，

所以在Rt△MBA′中，cos(π－2θ)＝＝，

所以x＝.

由于△AMN為等邊三角形，

所以綠地的面積

S＝2××a×a×sin＝a2.

(2)因為在Rt△ABC中，∠B＝，AB＝a，BC＝a，

所以∠BAC＝，所以在△AMN中，∠ANM＝－θ，

由正弦定理得＝，

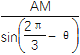設AM＝ax(0<x<1)，則A′M＝ax，BM＝a－ax，

所以在Rt△MBA′中，cos(π－2θ)＝＝，

所以x＝，即AM＝，

所以AN＝.

2sinθsin＝sin2θ＋sinθcosθ

＝＋sin2θ－cos2θ＝＋sin(2θ－)，

因為<θ<，所以<2θ－<，

所以當且僅當2θ－＝，即θ＝時，AN的值最小，且AN＝a，此時綠地公共走道的長度MN＝a.