
【題目】已知函數(shù)![]() (
(![]() ,且
,且![]() )在
)在![]() 上單調(diào)遞增,且關(guān)于
上單調(diào)遞增,且關(guān)于![]() 的方程
的方程![]() 恰有兩個不相等的實(shí)數(shù)解,則
恰有兩個不相等的實(shí)數(shù)解,則![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
由題意首先求得a的取值范圍,然后結(jié)合函數(shù)的解析式將原問題轉(zhuǎn)化為兩函數(shù)圖像存在兩個交點(diǎn)的問題,數(shù)形結(jié)合即可確定a的取值范圍.
由函數(shù)的解析式可知函數(shù)在區(qū)間![]() 上單調(diào)遞增,
上單調(diào)遞增,
當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 單調(diào)遞減,由復(fù)合函數(shù)的單調(diào)性法則可知:
單調(diào)遞減,由復(fù)合函數(shù)的單調(diào)性法則可知:![]() ,
,
且函數(shù)在![]() 處滿足:
處滿足:![]() ,解得:
,解得:![]() ,故
,故![]() ,
,
方程![]() 恰有兩個不相等的實(shí)數(shù)解,則函數(shù)
恰有兩個不相等的實(shí)數(shù)解,則函數(shù)![]() 與函數(shù)
與函數(shù)![]() 的圖像有且僅有兩個不同的交點(diǎn),
的圖像有且僅有兩個不同的交點(diǎn),
繪制函數(shù)![]() 的圖像如圖中虛線所示,
的圖像如圖中虛線所示,
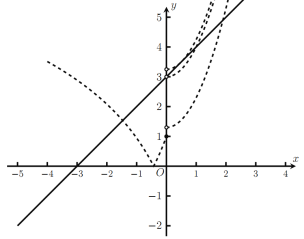
令![]() 可得:
可得:![]() ,
,
由![]() 可知
可知![]() ,
,![]() ,
,
則直線![]() 與函數(shù)
與函數(shù)![]() 的圖像在區(qū)間
的圖像在區(qū)間![]() 上存在唯一的交點(diǎn),
上存在唯一的交點(diǎn),
原問題轉(zhuǎn)化為函數(shù)![]() 與二次函數(shù)
與二次函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上存在唯一的交點(diǎn),
上存在唯一的交點(diǎn),
很明顯當(dāng)![]() ,即
,即![]() 時滿足題意,
時滿足題意,
當(dāng)直線與二次函數(shù)相切時,設(shè)切點(diǎn)坐標(biāo)為![]() ,亦即
,亦即![]() ,
,
由函數(shù)的解析式可得:![]() ,故:
,故:![]() ,則
,則![]() ,
,
切點(diǎn)坐標(biāo)為![]() ,從而:
,從而:![]() ,即
,即![]() .
.
據(jù)此可得:![]() 的取值范圍是
的取值范圍是![]() .
.
故選:D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】點(diǎn)![]() 、
、![]() 、
、![]() 分別是正方體
分別是正方體![]() 的棱
的棱![]() ,
,![]() ,
,![]() 的中點(diǎn),則下列命題中的真命題是__________(寫出所有真命題的序號).
的中點(diǎn),則下列命題中的真命題是__________(寫出所有真命題的序號).
①以正方體的頂點(diǎn)為頂點(diǎn)的三棱錐的四個面中最多可以四個面都是直角三角形;
②點(diǎn)![]() 在直線
在直線![]() 上運(yùn)動時,總有
上運(yùn)動時,總有![]() ;
;
③點(diǎn)![]() 在直線
在直線![]() 上運(yùn)動時,三棱錐
上運(yùn)動時,三棱錐![]() 的體積是定值;
的體積是定值;
④若![]() 是正方體的面
是正方體的面![]() ,(含邊界)內(nèi)一動點(diǎn),且點(diǎn)
,(含邊界)內(nèi)一動點(diǎn),且點(diǎn)![]() 到點(diǎn)
到點(diǎn)![]() 和
和![]() 的距離相等,則點(diǎn)
的距離相等,則點(diǎn)![]() 的軌跡是一條線段.
的軌跡是一條線段.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】C反應(yīng)蛋白(CRP)是機(jī)體受到微生物入侵或組織損傷等炎癥性刺激時細(xì)胞合成的急性相蛋白,醫(yī)學(xué)認(rèn)為CRP值介于0-10mg/L為正常值.下面是某患者在治療期間連續(xù)5天的檢驗(yàn)報(bào)告單中CRP值(單位:mg/L)與治療大數(shù)的統(tǒng)計(jì)數(shù)據(jù):
治療天數(shù)x | 1 | 2 | 3 | 4 | 5 |
CRP值y | 51 | 40 | 35 | 28 | 21 |
(1)若CRP值y與治療數(shù)x只有線性相關(guān)關(guān)系試用最小乘法求出y關(guān)于x的線性回歸方程,并估計(jì)該者至少需要治療多少天CRP值可以回到正常水平;
(2)為均衡城鄉(xiāng)保障待遇,統(tǒng)一保障范同和支付準(zhǔn),為多保人員提供公平的基本醫(yī)療保障.某市城鄉(xiāng)醫(yī)療保險(xiǎn)實(shí)施辦法指出:門診報(bào)銷比例為50%;住院報(bào)銷比例,A類醫(yī)療機(jī)構(gòu)80%,B類醫(yī)療機(jī)構(gòu)60%.若張華參加了城鄉(xiāng)基本醫(yī)療保險(xiǎn),他因CRP偏高選擇在醫(yī)療機(jī)構(gòu)治療,醫(yī)生為張華提供了三種治療方案:方案一:門診治療,預(yù)計(jì)每天診療費(fèi)80元;方案二:住院治療,A類醫(yī)療機(jī)構(gòu),入院檢查需花費(fèi)600元,預(yù)計(jì)每天診療費(fèi)100元;方案三:住院治療,B類醫(yī)療機(jī)構(gòu),入院檢查需花費(fèi)400元,預(yù)計(jì)每天診療費(fèi)40元;若張華需要經(jīng)過連續(xù)治療n天![]() ,請你為張華選擇最經(jīng)濟(jì)實(shí)惠的治療方案.
,請你為張華選擇最經(jīng)濟(jì)實(shí)惠的治療方案.
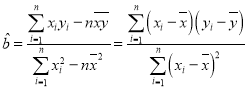 ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】C反應(yīng)蛋白(CRP)是機(jī)體受到微生物入侵或組織損傷等炎癥性刺激時肝細(xì)胞合成的急性相蛋白,醫(yī)學(xué)認(rèn)為CRP值介于0-10mg/L為正常值下面是某患者在治療期間連續(xù)5天的檢驗(yàn)報(bào)告單中CRP值(單位:mg/L)與治療天數(shù)的統(tǒng)計(jì)數(shù)據(jù):
治療天數(shù)x | 1 | 2 | 3 | 4 | 5 |
CRP值y | 51 | 40 | 35 | 28 | 21 |
(1)若CRP值y與治療天數(shù)x具有線性相關(guān)關(guān)系,試用最小二乘法求出y關(guān)于x的線性回歸方程,并估計(jì)該患者至少需要治療多少天CRP值可以到正常水平;
(2)為均衡城鄉(xiāng)保障待遇,統(tǒng)一保障范圍和支付標(biāo)準(zhǔn),為參保人員提供公平的基本醫(yī)療保障.某市城鄉(xiāng)醫(yī)療保險(xiǎn)實(shí)施辦法指出:門診報(bào)銷比例為50%:住院報(bào)銷比例,A類醫(yī)療機(jī)構(gòu)80%,B類醫(yī)療機(jī)構(gòu)60%.若張華參加了城鄉(xiāng)基本醫(yī)療保險(xiǎn),他因CRP偏高選擇在某醫(yī)療機(jī)構(gòu)治療,醫(yī)生為張華提供了三種治療方案:
方案一:門診治療,預(yù)計(jì)每天診療費(fèi)80元;
方案二:住院治療,A類醫(yī)療機(jī)構(gòu),入院檢查需花費(fèi)600元,預(yù)計(jì)每天診療費(fèi)100元;
方案三:住院治療,B類醫(yī)療機(jī)構(gòu),入院檢查需花費(fèi)400元,預(yù)計(jì)每天診療費(fèi)40元;
若張華需要經(jīng)過連續(xù)治療n天,![]() ,請你為張華選擇最經(jīng)濟(jì)實(shí)惠的治療方案.
,請你為張華選擇最經(jīng)濟(jì)實(shí)惠的治療方案.
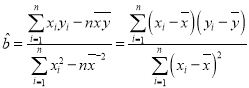 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列五個命題:
①“![]() ”是“
”是“![]() 為R上的增函數(shù)”的充分不必要條件;
為R上的增函數(shù)”的充分不必要條件;
②函數(shù)![]() 有兩個零點(diǎn);
有兩個零點(diǎn);
③集合A={2,3},B={1,2,3},從A,B中各任意取一個數(shù),則這兩數(shù)之和等于4的概率是![]() ;
;
④動圓C即與定圓![]() 相外切,又與y軸相切,則圓心C的軌跡方程是
相外切,又與y軸相切,則圓心C的軌跡方程是![]()
⑤若對任意的正數(shù)x,不等式![]() 恒成立,則實(shí)數(shù)
恒成立,則實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]()
其中正確的命題序號是_____.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】![]() 是衡量空氣污染程度的一個指標(biāo),為了了解
是衡量空氣污染程度的一個指標(biāo),為了了解![]() 市空氣質(zhì)量情況,從
市空氣質(zhì)量情況,從![]() 年每天的
年每天的![]() 值的數(shù)據(jù)中隨機(jī)抽取
值的數(shù)據(jù)中隨機(jī)抽取![]() 天的數(shù)據(jù),其頻率分布直方圖如圖所示.將
天的數(shù)據(jù),其頻率分布直方圖如圖所示.將![]() 值劃分成區(qū)間
值劃分成區(qū)間![]() 、
、![]() 、
、![]() 、
、![]() ,分別稱為一級、二級、三級和四級,統(tǒng)計(jì)時用頻率估計(jì)概率 .
,分別稱為一級、二級、三級和四級,統(tǒng)計(jì)時用頻率估計(jì)概率 .

(1)根據(jù)![]() 年的數(shù)據(jù)估計(jì)該市在
年的數(shù)據(jù)估計(jì)該市在![]() 年中空氣質(zhì)量為一級的天數(shù);
年中空氣質(zhì)量為一級的天數(shù);
(2)如果![]() 市對環(huán)境進(jìn)行治理,經(jīng)治理后,每天
市對環(huán)境進(jìn)行治理,經(jīng)治理后,每天![]() 值
值![]() 近似滿足正態(tài)分布
近似滿足正態(tài)分布![]() ,求經(jīng)過治理后的
,求經(jīng)過治理后的![]() 值的均值下降率.
值的均值下降率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】畫糖是一種以糖為材料在石板上進(jìn)行造型的民間藝術(shù),常見于公園與旅游景點(diǎn).某師傅制作了一種新造型糖畫,為了進(jìn)行合理定價(jià)先進(jìn)性試銷售,其單價(jià)![]() (元)與銷量
(元)與銷量![]() (個)相關(guān)數(shù)據(jù)如下表:
(個)相關(guān)數(shù)據(jù)如下表:

(1)已知銷量![]() 與單價(jià)
與單價(jià)![]() 具有線性相關(guān)關(guān)系,求
具有線性相關(guān)關(guān)系,求![]() 關(guān)于
關(guān)于![]() 的線性相關(guān)方程;
的線性相關(guān)方程;
(2)若該新造型糖畫每個的成本為![]() 元,要使得進(jìn)入售賣時利潤最大,請利用所求的線性相關(guān)關(guān)系確定單價(jià)應(yīng)該定為多少元?(結(jié)果保留到整數(shù))
元,要使得進(jìn)入售賣時利潤最大,請利用所求的線性相關(guān)關(guān)系確定單價(jià)應(yīng)該定為多少元?(結(jié)果保留到整數(shù))
參考公式:線性回歸方程![]() 中斜率和截距最小二乘法估計(jì)計(jì)算公式:
中斜率和截距最小二乘法估計(jì)計(jì)算公式:

![]() .參考數(shù)據(jù):
.參考數(shù)據(jù):![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com