【題目】在△ABC中，內角A，B，C所對的邊分別為a，b，c，且
．
（1）求角A；
（2）若a＝2，△ABC的周長為6，求△ABC的面積．
【答案】（1）
； （2）
.
【解析】
(1)利用正弦定理邊角互化與和差角公式化簡求
即可.
(2)利用a＝2,△ABC的周長為6可求出b+c＝4.再用余弦定理與化簡出關于
的表達式從而得出
再求解面積即可.
（1）∵
,
∴由正弦定理可得3sinAcosB
sinBsinA＝3sinC,
∵sinC＝sin（A+B）＝sinAcosB+sinBcosA,
∴
sinBsinA＝3cosAsinB,
∵sinB≠0,∴sinA＝3cosA,可得tanA
,
∵A∈（0,π）,∴A
．
（2）∵A,a＝2,△ABC的周長為6,
∴b+c＝4,
∴由余弦定理a2＝b2+c2﹣2bccosA,可得4＝b2+c2﹣bc＝（b+c）2﹣3bc＝16﹣3bc,解得bc＝4,
∴S△ABC
bcsinA
．
津橋教育計算小狀元系列答案科目：高中數學 來源： 題型：
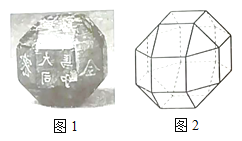
【題目】中國有悠久的金石文化，印信是金石文化的代表之一．印信的形狀多為長方體、正方體或圓柱體，但南北朝時期的官員獨孤信的印信形狀是“半正多面體”（圖1）.半正多面體是由兩種或兩種以上的正多邊形圍成的多面體.半正多面體體現了數學的對稱美．圖2是一個棱數為48的半正多面體，它的所有頂點都在同一個正方體的表面上，且此正方體的棱長為1．則該半正多面體共有________個面，其棱長為_________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若函數y=f（x）在區間D上是增函數，且函數y=
在區間D上是減函數，則稱函數f（x）是區間D上的“H函數”．對于命題：
①函數f（x）=-x+
是區間（0，1）上的“H函數”；
②函數g（x）=
是區間（0，1）上的“H函數”．下列判斷正確的是（ ）
A. 
和
均為真命題 B. 為真命題，為假命題
C. 為假命題，為真命題 D. 和均為假命題
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解甲、乙兩種離子在小鼠體內的殘留程度，進行如下試驗：將200只小鼠隨機分成
兩組，每組100只，其中
組小鼠給服甲離子溶液，
組小鼠給服乙離子溶液.每只小鼠給服的溶液體積相同、摩爾濃度相同.經過一段時間后用某種科學方法測算出殘留在小鼠體內離子的百分比.根據試驗數據分別得到如下直方圖：
記
為事件：“乙離子殘留在體內的百分比不低于
”，根據直方圖得到
的估計值為
.
（1）求乙離子殘留百分比直方圖中
的值；
（2）分別估計甲、乙離子殘留百分比的平均值（同一組中的數據用該組區間的中點值為代表）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】華為手機作為華為公司三大核心業務之一，2018年的銷售量躍居全球第二名，某機構隨機選取了100名華為手機的顧客進行調查，并將這
人的手機價格按照
，
，…
分成
組，制成如圖所示的頻率分布直方圖，其中
是
的
倍.
（1）求，的值；
（2）求這名顧客手機價格的平均數（同一組中的數據用該組區間的中間值作代表）；
（3）利用分層抽樣的方式從手機價格在和
的顧客中選取
人，并從這人中隨機抽取人進行回訪，求抽取的人手機價格在不同區間的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】李明自主創業，在網上經營一家水果店，銷售的水果中有草莓、京白梨、西瓜、桃，價格依次為60元/盒、65元/盒、80元/盒、90元/盒．為增加銷量，李明對這四種水果進行促銷：一次購買水果的總價達到120元，顧客就少付x元．每筆訂單顧客網上支付成功后，李明會得到支付款的80%．
①當x=10時，顧客一次購買草莓和西瓜各1盒，需要支付__________元；
②在促銷活動中，為保證李明每筆訂單得到的金額均不低于促銷前總價的七折，則x的最大值為__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義首項為1且公比為正數的等比數列為“M－數列”.
（1）已知等比數列{an}滿足：
，求證:數列{an}為“M－數列”；
（2）已知數列{bn}滿足:
，其中Sn為數列{bn}的前n項和．
①求數列{bn}的通項公式；
②設m為正整數，若存在“M－數列”{cn}
，對任意正整數k，當k≤m時，都有
成立，求m的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
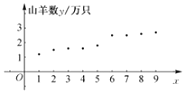
【題目】某縣畜牧技術員張三和李四9年來一直對該縣山羊養殖業的規模進行跟蹤調查，張三提供了該縣某山羊養殖場年養殖數量
單位：萬只
與相應年份
序號的數據表和散點圖
如圖所示，根據散點圖，發現y與x有較強的線性相關關系，李四提供了該縣山羊養殖場的個數
單位：個關于x的回歸方程
．
年份序號x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
年養殖山羊 |
|
|
|
|
|
|
|
|
|
根據表中的數據和所給統計量，求y關于x的線性回歸方程參考統計量：
，
；
試估計：
該縣第一年養殖山羊多少萬只
到第幾年，該縣山羊養殖的數量與第一年相比縮小了？
附：對于一組數據
，
，
，其回歸直線
的斜率和截距的最小二乘估計分別為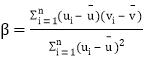
，
．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
