
【題目】若直線ax﹣by+2=0(a>0,b>0)被圓x2+y2+4x﹣4y﹣1=0所截得的弦長為6,則 ![]() 的最小值為( )
的最小值為( )
A.10
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:圓x2+y2+4x﹣4y﹣1=(x+2)2+(y﹣2)2=9是以(﹣2,2)為圓心,以3為半徑的圓,
又∵直線ax﹣by+2=0(a>0,b>0)被圓x2+y2+4x﹣4y﹣1=0所截得的弦長為6,
∴直線過圓心,
∴a+b=1,
∴ ![]() =(
=( ![]() )(a+b)=5+
)(a+b)=5+ ![]() ≥5+2
≥5+2 ![]() =5+2
=5+2 ![]() ,當且僅當a=
,當且僅當a= ![]() ﹣2,b=3﹣
﹣2,b=3﹣ ![]() 時取等號,
時取等號,
∴ ![]() 的最小值的最小值為5+2
的最小值的最小值為5+2 ![]() ,
,
故選:C.
由已知中圓的方程x2+y2+4x﹣4y﹣1=0我們可以求出圓心坐標,及圓的半徑,結合直線ax﹣by+2=0(a>0,b>0)被圓x2+y2+4x﹣4y﹣1=0所截得的弦長為6,我們易得到a,b的關系式,再根據基本不等式中1的活用,即可得到答案.


科目:高中數學 來源: 題型:
【題目】如圖,已知PA⊥⊙O所在的平面,AB是⊙O的直徑,AB=2,C是⊙O上一點,且AC=BC,PC與⊙O所在的平面成45°角,E是PC中點.F為PB中點. 
(1)求證:EF∥面ABC;
(2)求證:EF⊥面PAC;
(3)求三棱錐B﹣PAC的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某紡紗廠生產甲、乙兩種棉紗,已知生產甲種棉紗1噸需耗一級籽棉2噸、二級籽棉1噸;生產乙種棉紗1噸需耗一級籽棉1噸,二級籽棉2噸.每1噸甲種棉紗的利潤為900元,每1噸乙種棉紗的利潤為600元.工廠在生產這兩種棉紗的計劃中,要求消耗一級籽棉不超過250噸,二級籽棉不超過300噸.問甲、乙兩種棉紗應各生產多少噸,能使利潤總額最大?并求出利潤總額的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形ABCD 中,AD⊥平面ABE,AE=FB=BC=2,F為CE上的點,且BF⊥平面ACE,AC,BD交于G點 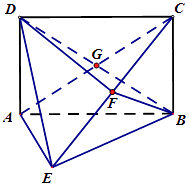
(1)求證:AE∥平面BFD
(2)求證:AE⊥平面BCE
(3)求三棱柱C﹣BGF的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的長軸長為6,且橢圓
的長軸長為6,且橢圓![]() 與圓
與圓![]() :
: ![]() 的公共弦長為
的公共弦長為![]() .
.
(1)求橢圓![]() 的方程.
的方程.
(2)過點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩點
交于兩點![]() ,
, ![]() ,試判斷在
,試判斷在![]() 軸上是否存在點
軸上是否存在點![]() ,使得
,使得![]() 為以
為以![]() 為底邊的等腰三角形.若存在,求出點
為底邊的等腰三角形.若存在,求出點![]() 的橫坐標的取值范圍,若不存在,請說明理由.
的橫坐標的取值范圍,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是平行四邊形,
是平行四邊形,![]() ,側面
,側面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
, ![]() 分別為
分別為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上.
上.

(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)如果直線![]() 與平面
與平面![]() 所成的角和直線
所成的角和直線![]() 與平面
與平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com