
【題目】某市每年春節前后,由于大量的煙花炮竹的燃放,空氣污染較為嚴重.該市環保研究所對近年春節前后每天的空氣污染情況調查研究后發現,每天空氣污染的指數.f(t),隨時刻t(時)變化的規律滿足表達式![]() ,其中a為空氣治理調節參數,且a∈(0,1).
,其中a為空氣治理調節參數,且a∈(0,1).
(1)令![]() ,求x的取值范圍;
,求x的取值范圍;
(2)若規定每天中f(t)的最大值作為當天的空氣污染指數,要使該市每天的空氣污染指數不超過5,試求調節參數a的取值范圍.
【答案】(1)[0,1];(2)![]() .
.
【解析】
(1)題根據t的取值范圍,及復合函數同增的單調性可得x的取值范圍;
(2)題根據第(1)題的提示構造一個函數h(x)=|x-a|+3a+2,然后將絕對值函數轉化成分段函數,考慮單調性及最大值的取值,再與5比較,即可得到調節參數a的取值范圍.
(1)由題意,0≤t≤24,則1≤![]() t+1≤10,
t+1≤10,
∴0=lg1≤lg(![]() t+1)≤lg10=1.
t+1)≤lg10=1.
故x的取值范圍為:[0,1].
(2)由(1),知: ![]()
可設![]()
則![]() .
.
根據一次函數的單調性,很明顯h(x)在[0,a)上單調遞減,在[a,1]上單調遞增.
∴用![]() 表示函數的最大值是
表示函數的最大值是![]() 中最大的值.
中最大的值.
∵![]() ,
,
∴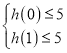 ,即
,即![]() ,
,
解得0<a≤![]() .
.
∴a的取值范圍為:(0,![]() ].
].


科目:高中數學 來源: 題型:
【題目】以![]() 表示值域為
表示值域為![]() 的函數組成的集合,
的函數組成的集合,![]() 表示具有如下性質的函數
表示具有如下性質的函數![]() 組成的集合:對于函數
組成的集合:對于函數![]() ,存在一個正數
,存在一個正數![]() ,使得函數
,使得函數![]() 的值域包含于區間
的值域包含于區間![]() 。例如,當
。例如,當![]() ,
,![]() 時,
時,![]() ,
,![]() 。則下列命題中正確的是:( )
。則下列命題中正確的是:( )
A.設函數![]() 的定義域為
的定義域為![]() ,則“
,則“![]() ”的充要條件是“
”的充要條件是“![]() ,
,![]() ,
,![]() ”
”
B.函數![]() 的充要條件是
的充要條件是![]() 有最大值和最小值
有最大值和最小值
C.若函數![]() ,
,![]() 的定義域相同,且
的定義域相同,且![]() ,
,![]() ,則
,則![]()
D.若函數![]() 有最大值,則
有最大值,則![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數是上一層燈數的2倍,則塔的頂層共有燈( )
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系中,曲線![]() 的參數方程是
的參數方程是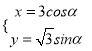 (
(![]() 為參數)以原點為極點,
為參數)以原點為極點, ![]() 軸正半軸為極軸,并取與直角坐標系相同的單位長度,建立極坐標系,曲線
軸正半軸為極軸,并取與直角坐標系相同的單位長度,建立極坐標系,曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)求曲線![]() ,
, ![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 、
、![]() 分別是曲線
分別是曲線![]() 和
和![]() 上的任意點,求
上的任意點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖是改革開放四十周年大型展覽的展館--------國家博物館.現欲測量博物館正門柱樓頂部一點![]() 離地面的高度
離地面的高度![]() (點
(點![]() 在柱樓底部).在地面上的兩點
在柱樓底部).在地面上的兩點![]() ,
,![]() 測得點
測得點![]() 的仰角分別為
的仰角分別為![]() ,
,![]() ,且
,且![]() ,
,![]() 米,則
米,則![]() 為( )
為( )

A. 10米 B. 20米 C. 30米 D. 40米
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】提升城市道路通行能力,可為市民提供更多出行便利.我校某研究性學習小組對成都市一中心路段(限行速度為![]() 千米/小時)的擁堵情況進行調查統計,通過數據分析發現:該路段的車流速度
千米/小時)的擁堵情況進行調查統計,通過數據分析發現:該路段的車流速度![]() (輛/千米)與車流密度
(輛/千米)與車流密度![]() (千米/小時)之間存在如下關系:如果車流密度不超過
(千米/小時)之間存在如下關系:如果車流密度不超過![]() 該路段暢通無阻(車流速度為限行速度);當車流密度在
該路段暢通無阻(車流速度為限行速度);當車流密度在![]() 時,車流速度是車流密度的一次函數;車流密度一旦達到
時,車流速度是車流密度的一次函數;車流密度一旦達到![]() 該路段交通完全癱瘓(車流速度為零).
該路段交通完全癱瘓(車流速度為零).
(1)求![]() 關于
關于![]() 的函數
的函數![]()
(2)已知車流量(單位時間內通過的車輛數)等于車流密度與車流速度的乘積,求此路段車流量的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著人口老齡化的到來,我國的勞動力人口在不斷減少,“延遲退休”已經成為人們越來越關注的話題,為了解公眾對“延遲退休”的態度,某校課外研究性學習小組在某社區隨機抽取了50人進行調查,將調查情況進行整理后制成下表:
年齡 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
人數 | 4 | 5 | 8 | 5 | 3 |
年齡 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
人數 | 6 | 7 | 3 | 5 | 4 |
經調查年齡在[25,30),[55,60)的被調查者中贊成“延遲退休”的人數分別是3人和2人.現從這兩組的被調查者中各隨機選取2人,進行跟蹤調查.
(I)求年齡在[25,30)的被調查者中選取的2人都贊成“延遲退休”的概率;
(II)若選中的4人中,不贊成“延遲退休”的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某船在![]() 處測得燈塔
處測得燈塔![]() 在其南偏東
在其南偏東![]() 方向上,該船繼續向正南方向行駛5海里到
方向上,該船繼續向正南方向行駛5海里到![]() 處,測得燈塔在其北偏東
處,測得燈塔在其北偏東![]() 方向上,然后該船向東偏南
方向上,然后該船向東偏南![]() 方向行駛2海里到
方向行駛2海里到![]() 處,此時船到燈塔
處,此時船到燈塔![]() 的距離為多少海里( )
的距離為多少海里( )
A.![]() 千米B.
千米B.![]() 千米C.6千米D.5千米
千米C.6千米D.5千米
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種蔬菜從1月1日起開始上市,通過市場調查,得到該蔬菜種植成本![]() (單位:元/
(單位:元/![]() )與上市時間
)與上市時間![]() (單位:10天)的數據如下表:
(單位:10天)的數據如下表:
時間 | 5 | 11 | 25 |
種植成本 | 15 | 10.8 | 15 |
(1)根據上表數據,從下列函數:![]() ,
,![]() ,
,![]() ,
,![]() 中(其中
中(其中![]() ),選取一個合適的函數模型描述該蔬菜種植成本
),選取一個合適的函數模型描述該蔬菜種植成本![]() 與上市時間
與上市時間![]() 的變化關系;
的變化關系;
(2)利用你選取的函數模型,求該蔬菜種植成本最低時的上市時間及最低種植成本.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com