【題目】先后拋擲兩枚質地均勻的骰子各一次，設出現的點數之和是12，11，10的概率依次是
，
，
，則( )
A. =< B. <<
C. <= D. =<
【答案】B
【解析】
我們列出先后拋擲兩枚骰子出現的點數的所有的基本事件個數，再分別求出點數之和是12、11、10的基本事件個數，進而求出點數之和是12、11、10的概率P1、P2、P3，即可得到它們的大小關系．
我們列出先后拋擲兩枚質地均勻的骰子各一次出現的點數的所有的基本事件個數，再分別求出點數之和是12，11，10的基本事件個數，進而求出點數之和是12，11，10的概率
，
，
，即可得到它們的大小關系．先后拋擲兩枚質地均勻的骰子各一次，出現的點數有：（1，1），（1，2），（1，3），（1，4），（1，5），（1，6），（2，1），（2，2），（2，3），（2，4），（2，5），（2，6），（3，1），（3，2），（3，3），（3，4），（3，5），（3，6），（4，1），（4，2），（4，3），（4，4），（4，5），（4，6），（5，1），（5，2），（5，3），（5，4），（5，5），（5，6），（6，1），（6，2），（6，3），（6，4），（6，5），（6，6），共36種，其中點數之和是12的有1種，故=
；點數之和是11的有2種，故=
=
；點數之和是10的有3種，故=
=
，故＜＜，
故選：B.
科目：高中數學 來源： 題型：
【題目】如圖，圓內接四邊形ABCD中，BD是圓的直徑，AB=AC，延長AD與BC的延長線相交于點E，作EF⊥BD于F． 
（1）證明：EC=EF；
（2）如果DC= 
BD=3，試求DE的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設拋物線
的焦點為F，動點P在直線
上運動，過P作拋物線C的兩條切線PA、PB，且與拋物線C分別相切于A、B兩點.
（1）求△APB的重心G的軌跡方程.
（2）證明∠PFA=∠PFB.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，Rt△AOB的直角邊OA在x軸上，OA=2，AB=1，將Rt△AOB繞點O逆時針旋轉90°得到
，拋物線
經過B、D兩點．
（1）求二次函數的解析式；
（2）連接BD，點P是拋物線上一點，直線OP把△BOD的周長分成相等的兩部分，求點P的坐標．
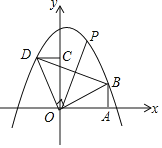
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}滿足0＜an＜1，且an+1+ 
=2an+ 
（n∈N*）．
（1）證明：an+1＜an；
（2）若a1= 
，設數列{an}的前n項和為Sn ， 證明： 
﹣ 
＜Sn＜ 
﹣2．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在5件產品中，有3件一等品和2件二等品，從中任取2件，以
為概率的事件是( )
A. 恰有1件一等品 B. 至少有一件一等品
C. 至多有一件一等品 D. 都不是一等品
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知集合Z＝{(x，y)|x∈[0，2]，y∈[－1，1]}.
(1)若x，y∈Z，求x＋y≥0的概率；
(2)若x，y∈R，求x＋y≥0的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知：函數
．
（1）當
時，求函數
的極值；
（2）若函數
，討論
的單調性；
（3）若函數
的圖象與
軸交于兩點
，且
．設
，其中常數
、
滿足條件
，且
．試判斷在點
處的切線斜率的正負，并說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
