
【題目】某企業生產A、B兩種產品,生產每一噸產品所需的勞動力和煤、電耗如下表:
產品品種 | 勞動力 | 煤 | 電 |
A產品 | 3 | 9 | 4 |
B產品 | 10 | 4 | 5 |
已知生產每噸A產品的利潤是7萬元,生產每噸B產品的利潤是12萬元,現在條件有限,該企業僅有勞動力300個,煤360噸,并且供電局只能供電200千瓦,試問:該企業生產A、B兩種產品各多少噸,才能獲得最大利潤?并求出最大利潤.
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數是上一層燈數的2倍,則塔的頂層共有燈( )
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
:![]() 關于直線
關于直線![]() 對稱且過點
對稱且過點![]() 和
和![]() ,直線
,直線![]() 過定點
過定點![]() .
.
(1)證明:直線![]() 與圓
與圓![]() 相交;
相交;
(2)記直線![]() 與圓
與圓![]() 的兩個交點為
的兩個交點為![]() ,
,![]() .
.
①若弦長![]() ,求直線方程;
,求直線方程;
②求![]() 面積的最大值及
面積的最大值及![]() 面積的最大時的直線方程.
面積的最大時的直線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點P和非零實數![]() ,若兩條不同的直線
,若兩條不同的直線![]() 均過點P,且斜率之積為
均過點P,且斜率之積為![]() ,則稱直線
,則稱直線![]() 是一組“
是一組“![]() 共軛線對”,如直
共軛線對”,如直![]() 是一組“
是一組“![]() 共軛線對”,其中O是坐標原點.
共軛線對”,其中O是坐標原點.
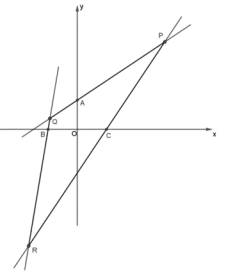
(1)已知![]() 是一組“
是一組“![]() 共軛線對”,求
共軛線對”,求![]() 的夾角的最小值;
的夾角的最小值;
(2)已知點A(0,1)、點![]() 和點C(1,0)分別是三條直線PQ,QR,RP上的點(A,B,C與P,Q,R均不重合),且直線PR,PQ是“
和點C(1,0)分別是三條直線PQ,QR,RP上的點(A,B,C與P,Q,R均不重合),且直線PR,PQ是“![]() 共軛線對”,直線QP,QR是“
共軛線對”,直線QP,QR是“![]() 共軛線對”,直線RP,RQ是“
共軛線對”,直線RP,RQ是“![]() 共軛線對”,求點P的坐標;
共軛線對”,求點P的坐標;
(3)已知點![]() ,直線
,直線![]() 是“
是“![]() 共軛線對”,當
共軛線對”,當![]() 的斜率變化時,求原點O到直線
的斜率變化時,求原點O到直線![]() 的距離之積的取值范圍.
的距離之積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市![]() 戶居民的月平均用電量(單位:度),以
戶居民的月平均用電量(單位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分組的頻率分布直方圖如圖.
分組的頻率分布直方圖如圖.

(1)求直方圖中![]() 的值;
的值;
(2)求月平均用電量的眾數和中位數;
(3)在月平均用電量為![]() ,
,![]() ,
,![]() ,
,![]() 的四組用戶中,用分層抽樣的方法抽取
的四組用戶中,用分層抽樣的方法抽取![]() 戶居民,則月平均用電量在
戶居民,則月平均用電量在![]() 的用戶中應抽取多少戶?
的用戶中應抽取多少戶?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】邊長為1的正方形![]() (及其內部)繞的
(及其內部)繞的![]() 旋轉一周形成圓柱,如圖,
旋轉一周形成圓柱,如圖,![]() 長為
長為![]() ,
,![]() 長為
長為![]() ,其中
,其中![]() 與
與![]() 在平面
在平面![]() 的同側.
的同側.
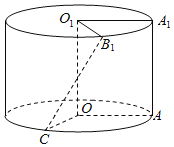
(1)求二面角![]() 的大小;(結果用反三角函數值表示)
的大小;(結果用反三角函數值表示)
(2)用一平行于![]() 的平面去截這個圓柱,若該截面把圓柱側面積分成
的平面去截這個圓柱,若該截面把圓柱側面積分成![]() 兩部分,求
兩部分,求![]() 與該截面的距離;
與該截面的距離;
(3)求線段![]() ,
,![]() 繞著
繞著![]() 旋轉
旋轉![]() 所形成的幾何體的表面積.
所形成的幾何體的表面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著城市地鐵建設的持續推進,市民的出行也越來越便利,根據大數據統計,某條地鐵線路運行時,發車時間間隔![]() (單位:分鐘)滿足:
(單位:分鐘)滿足: ![]() ,平均每班地鐵的載客人數
,平均每班地鐵的載客人數![]() (單位:人)與發車時間間隔
(單位:人)與發車時間間隔![]() 近似地滿足函數關系:
近似地滿足函數關系: ,
,
(1)若平均每班地鐵的載客人數不超過1560人,試求發車時間間隔![]() 的取值范圍;
的取值范圍;
(2)若平均每班地鐵每分鐘的凈收益為![]() (單位:元),則當發車時間間隔
(單位:元),則當發車時間間隔![]() 為多少時,平均每班地鐵每分鐘的凈收益最大?并求出最大凈收益.
為多少時,平均每班地鐵每分鐘的凈收益最大?并求出最大凈收益.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com