
【題目】已知cos(π+α) ![]() =
= ![]() ,且
,且 ![]() <α<
<α< ![]() ,求sin α與cos α的值.
,求sin α與cos α的值.
【答案】解:cos(π+α)=﹣cos α, ![]() =﹣sin α. ∴sin αcos α=
=﹣sin α. ∴sin αcos α= ![]() ,即2sin αcos α=
,即2sin αcos α= ![]() ①
①
又∵sin2α+cos2α=1,②
②+①得(sin α+cos α)2= ![]() ,
,
②-①得(sin α﹣cos α)2= ![]() ,
,
又∵ ![]() <α<
<α< ![]() ,
,
∴sin α>cos α>0,
即sin α+cos α>0,sin α﹣cos α>0,
∴sin α+cos α= ![]() ,③
,③
sin α﹣cos α= ![]() ,④
,④
③+④得sin α= ![]() ,③-④得cos α=
,③-④得cos α= ![]()
【解析】由已知利用誘導公式可求2sin αcos α= ![]() ,結合同角三角函數基本關系式可求:(sin α+cos α)2=
,結合同角三角函數基本關系式可求:(sin α+cos α)2= ![]() ,(sin α﹣cos α)2=
,(sin α﹣cos α)2= ![]() ,結合α的范圍可求sin α+cos α>0,sin α﹣cos α>0,可求sin α+cos α=
,結合α的范圍可求sin α+cos α>0,sin α﹣cos α>0,可求sin α+cos α= ![]() ,sin α﹣cos α=
,sin α﹣cos α= ![]() ,聯立即可得解.
,聯立即可得解.
【考點精析】解答此題的關鍵在于理解兩角和與差的正弦公式的相關知識,掌握兩角和與差的正弦公式:![]() .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,b=
,b= ![]() .
.
(1)求橢圓C的標準方程;
(2)F1 , F2分別為橢圓的左、右焦點,A、B為橢圓的左、右頂點,P為橢圓C上的點,求證:以PF2為直徑的圓與以AB為直徑的圓相切;
(3)過左焦點F1作互相垂直的弦MN與GH,判斷MN的中點與GH的中點所在直線l是否過x軸上的定點,如果是,求出定點坐標,如果不是,說出理由. 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個盒子裝有六張卡片,上面分別寫著如下六個函數:
![]()
![]()
![]()
![]()
![]()
![]() .
.
(Ⅰ)從中任意拿取![]() 張卡片,其中至少有一張卡片上寫著的函數為奇函數,在此條件下,求兩張卡片上寫著的函數相加得到的新函數為奇函數的概率;
張卡片,其中至少有一張卡片上寫著的函數為奇函數,在此條件下,求兩張卡片上寫著的函數相加得到的新函數為奇函數的概率;
(Ⅱ)現從盒子中逐一抽取卡片,且每次取出后均不放回,若取到一張寫有偶函數的卡片則停止抽取,否則繼續進行,求抽取次數![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為緩解高三學生的高考壓力,經常舉行一些心理素質綜合能力訓練活動,經過一段時間的訓練后從該年級800名學生中隨機抽取100名學生進行測試,并將其成績分為![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五個等級,統計數據如圖所示(視頻率為概率),根據以上抽樣調查數據,回答下列問題:
五個等級,統計數據如圖所示(視頻率為概率),根據以上抽樣調查數據,回答下列問題:
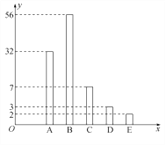
(1)試估算該校高三年級學生獲得成績為![]() 的人數;
的人數;
(2)若等級![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分別對應100分、90分、80分、70分、60分,學校要求平均分達90分以上為“考前心理穩定整體過關”,請問該校高三年級目前學生的“考前心理穩定整體”是否過關?
分別對應100分、90分、80分、70分、60分,學校要求平均分達90分以上為“考前心理穩定整體過關”,請問該校高三年級目前學生的“考前心理穩定整體”是否過關?
(3)為了解心理健康狀態穩定學生的特點,現從![]() 、
、![]() 兩種級別中,用分層抽樣的方法抽取11個學生樣本,再從中任意選取3個學生樣本分析,求這3個樣本為
兩種級別中,用分層抽樣的方法抽取11個學生樣本,再從中任意選取3個學生樣本分析,求這3個樣本為![]() 級的個數
級的個數![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC中,a、b、c分別為∠A,∠B,∠C的對邊,如果a、b、c成等差數列,∠B=30°,△ABC的面積為 ![]() ,那么b等于( )
,那么b等于( )
A.![]()
B.1+ ![]()
C.![]()
D.2+ ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
: ![]() 的焦點
的焦點![]() 也是橢圓
也是橢圓![]() :
: ![]() (
(![]() )的一個焦點,
)的一個焦點, ![]() 與
與![]() 的公共弦長為
的公共弦長為![]() .
.
(Ⅰ)求![]() 的方程
的方程
(Ⅱ)過點![]() 的直線
的直線![]() 與
與![]() 相交于
相交于![]() ,
, ![]() 兩點,與
兩點,與![]() 相交于
相交于![]() ,
, ![]() 兩點,且
兩點,且![]() ,
, ![]() 同向.若
同向.若![]() 求直線
求直線![]() 的斜率;
的斜率;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com