
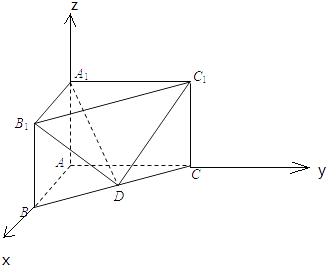
【題目】直三棱柱ABC﹣A1B1C1中,AB⊥AC,AB=2,AC=4,AA1=2,D為BC的中點.則直線DB1與平面A1C1D所成角的正弦值 .
【答案】![]()
【解析】解:分別以AB,AC,AA1所在直線為x,y,z軸,建立空間直角坐標系.
則A(0,0,0),B(2,0,0),
C(0,4,0),A1(0,0,2),B1(2,0,2),
C1(0,4,2),
∵D為BC的中點,∴D(1,2,0),![]() =(1,﹣2,2),
=(1,﹣2,2), ![]() (0,4,0),
(0,4,0), ![]() =(1,2,﹣2),
=(1,2,﹣2),
設平面A1C1D的法向量為 ![]() =(x,y,z),
=(x,y,z),
則 ![]() ,取x=2,
,取x=2,
得 ![]() =(2,0,1),
=(2,0,1),
又cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() ,
,
∴直線DB1與平面A1C1D所成角的正弦值為 ![]() .
.
所以答案是: ![]() .
.
【考點精析】解答此題的關鍵在于理解空間角的異面直線所成的角的相關知識,掌握已知![]() 為兩異面直線,A,C與B,D分別是
為兩異面直線,A,C與B,D分別是![]() 上的任意兩點,
上的任意兩點,![]() 所成的角為
所成的角為![]() ,則
,則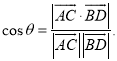 .
.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=( ![]() )x的圖象與函數g(x)的圖象關于直線y=x對稱,令h(x)=g(1﹣|x|),則關于h(x)有下列命題:
)x的圖象與函數g(x)的圖象關于直線y=x對稱,令h(x)=g(1﹣|x|),則關于h(x)有下列命題:
①h(x)的圖象關于原點對稱;
②h(x)為偶函數;
③h(x)的最小值為0;
④h(x)在(0,1)上為減函數.
其中正確命題的序號為:②③.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=kax(k為常數,a>0且a≠1)的圖象過點A(0,1)和點B(2,16).
(1)求函數的解析式;
(2)g(x)=b+ ![]() 是奇函數,求常數b的值;
是奇函數,求常數b的值;
(3)對任意的x1 , x2∈R且x1≠x2 , 試比較 ![]() 與
與 ![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知各項均為整數的數列{an}滿足an2≤1,1≤a12+a22+…+an2≤m,m,n∈N* .
(1)若m=1,n=2,寫出所有滿足條件的數列{an};
(2)設滿足條件的{an}的個數為f(n,m).
①求f(2,2)和f(2016,2016);
②若f(m+1,m)>2016,試求m的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga|x+1|(a>0且a≠1),當x∈(0,1)時,恒有f(x)<0成立,則函數g(x)=loga(﹣ ![]() x2+ax)的單調遞減區間是 .
x2+ax)的單調遞減區間是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設m,n∈R,定義在區間[m,n]上的函數f(x)=log2(4﹣|x|)的值域是[0,2],若關于t的方程( ![]() )|t|+m+1=0(t∈R)有實數解,則m+n的取值范圍是 .
)|t|+m+1=0(t∈R)有實數解,則m+n的取值范圍是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】解答
(1)集合M={1,2,(m2﹣3m﹣1)+(m2﹣5m﹣6)i},N={3,﹣1},M∩N={3},求實數m的值.
(2)已知12= ![]() ×1×2×3,12+22=
×1×2×3,12+22= ![]() ×2×3×5,12+22+32=
×2×3×5,12+22+32= ![]() ×3×4×7,12+22+32+42=
×3×4×7,12+22+32+42= ![]() ×4×5×9,由此猜想12+22+…+n2(n∈N*)的表達式并用數學歸納法證明.
×4×5×9,由此猜想12+22+…+n2(n∈N*)的表達式并用數學歸納法證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com