
【題目】一條直線上依次有三點![]() 、
、![]() 、
、![]() .一只獵犬在點
.一只獵犬在點![]() 發現一大兩小三只兔子從點
發現一大兩小三只兔子從點![]() 向兔穴(點
向兔穴(點![]() )前行,立即向它們追去.當兔子發現獵犬追趕后,急忙向兔穴奔跑,大兔為了提高速度,可叼著一只小兔奔跑(速度不變,且叼起與放下小兔所耽誤的時間不計).已知
)前行,立即向它們追去.當兔子發現獵犬追趕后,急忙向兔穴奔跑,大兔為了提高速度,可叼著一只小兔奔跑(速度不變,且叼起與放下小兔所耽誤的時間不計).已知![]() ,
,![]() ,獵犬、大兔、小兔奔跑的速度分別為
,獵犬、大兔、小兔奔跑的速度分別為![]() 、
、![]() 、
、![]() ,兔子前行的速度為
,兔子前行的速度為![]() .則三只兔子至多在離開點
.則三只兔子至多在離開點![]() ______
______![]() 時發現獵犬,才能恰在獵犬追上自己之前全部跑進兔穴.
時發現獵犬,才能恰在獵犬追上自己之前全部跑進兔穴.
 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的右焦點為
的右焦點為![]() ,上頂點為
,上頂點為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,且原點到直線
,且原點到直線![]() 的距離為
的距離為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若不經過點![]() 的直線
的直線![]() :
:![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,且與圓
兩點,且與圓![]() 相切.試探究
相切.試探究![]() 的周長是否為定值,若是,求出定值;若不是,請說明理由.
的周長是否為定值,若是,求出定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年8月18日,舉世矚目的第18屆亞運會在印尼首都雅加達舉行,為了豐富亞運會志愿者的業余生活,同時鼓勵更多的有志青年加入志愿者行列,大會主辦方決定對150名志愿者組織一次有關體育運動的知識競賽(滿分120分)并計劃對成績前15名的志愿者進行獎勵,現將所有志愿者的競賽成績制成頻率分布直方圖,如圖所示,若第三組與第五組的頻數之和是第二組的頻數的3倍,試回答以下問題:
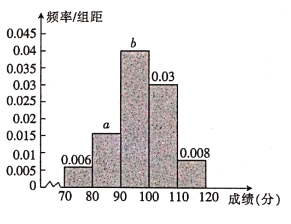
(1)求圖中![]() 的值;
的值;
(2)求志愿者知識競賽的平均成績;
(3)從受獎勵的15人中按成績利用分層抽樣抽取5人,再從抽取的5人中,隨機抽取2人在主會場服務,求抽取的這2人中其中一人成績在![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為迎接2022年北京冬季奧運會,普及冬奧知識,某校開展了“冰雪答題王”冬奧知識競賽活動.現從參加冬奧知識競賽活動的學生中隨機抽取了100名學生,將他們的比賽成績(滿分為100分)分為6組:![]() ,
,![]() 得到如圖所示的頻率分布直方圖.
得到如圖所示的頻率分布直方圖.
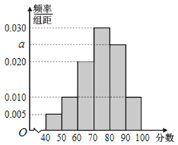
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)記![]() 表示事件“從參加冬奧知識競賽活動的學生中隨機抽取一名學生,該學生的比賽成績不低于80分”,估計
表示事件“從參加冬奧知識競賽活動的學生中隨機抽取一名學生,該學生的比賽成績不低于80分”,估計![]() 的概率;
的概率;
(Ⅲ)在抽取的100名學生中,規定:比賽成績不低于80分為“優秀”,比賽成績低于80分為“非優秀”.請在答題卡上將![]() 列聯表補充完整,并判斷是否有
列聯表補充完整,并判斷是否有![]() 的把握認為“比賽成績是否優秀與性別有關”?
的把握認為“比賽成績是否優秀與性別有關”?
參考公式及數據: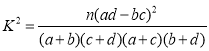 ,
,![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】復旦大學附屬華山醫院感染科主任醫師張文宏在接受媒體采訪時談到:通過救治研究發現,目前對于新冠肺炎最有用的“特效藥”還是免疫力.而人的免疫力與體質息息相關,一般來講,體質好,免疫力就強.復學已有一段時間,某醫院到學校調查高二學生的體質健康情況,隨機抽取12名高二學生進行體質健康測試,測試成績(百分制)如下:65,78,90,86,52,87,72,86,87,98,88,86.根據此年齡段學生體質健康標準,成績不低于80的為優良.
(1)將頻率視為概率,根據樣本估計總體的思想,在該學校全體高二學生中任選3人進行體質健康測試,求至少有1人成績是“優良”的概率;
(2)從抽取的12人中隨機選取3人,記![]() 表示成績“優良”的人數,求
表示成績“優良”的人數,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() 的離心率為
的離心率為![]() ,右焦點
,右焦點![]() 到右準線的距離為3.(橢圓的右準線方程為
到右準線的距離為3.(橢圓的右準線方程為![]() )
)
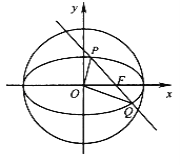
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設過![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點.已知
兩點.已知![]() 被圓
被圓![]() 截得的弦長為
截得的弦長為![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在直角坐標系xOy中,圓C的參數方程為![]() 為參數
為參數![]() ,以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為
,以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為![]() .
.
![]() 1
1![]() 求圓C的普通方程和直線l的直角坐標方程;
求圓C的普通方程和直線l的直角坐標方程;
![]() 2
2![]() 設M是直線l上任意一點,過M做圓C切線,切點為A、B,求四邊形AMBC面積的最小值.
設M是直線l上任意一點,過M做圓C切線,切點為A、B,求四邊形AMBC面積的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com