
【題目】已知點![]() 為拋物線
為拋物線![]() 的焦點,點
的焦點,點![]() 在拋物線
在拋物線![]() 上,且
上,且![]() .
.
(1)求拋物線![]() 的方程;
的方程;
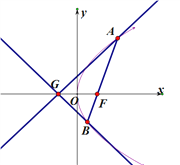
(2)已知點![]() ,延長
,延長![]() 交拋物線
交拋物線![]() 于點
于點![]() ,證明:以點
,證明:以點![]() 為圓心且與直線
為圓心且與直線![]() 相切的圓,必與直線
相切的圓,必與直線![]() 相切.
相切.
【答案】(Ⅰ)![]() ;(Ⅱ)詳見解析
;(Ⅱ)詳見解析
【解析】試題分析:解法一:(Ⅰ)由拋物線的定義得![]() .因為
.因為![]() ,即
,即![]() ,解得
,解得![]() ,即可求出拋物線
,即可求出拋物線![]() 的方程.(Ⅱ)因為點
的方程.(Ⅱ)因為點![]() 在拋物線
在拋物線![]()
![]() 上,所以
上,所以![]() ,由拋物線的對稱性,不妨設
,由拋物線的對稱性,不妨設![]() .由
.由![]() ,
, ![]() 可得直線
可得直線![]() 的方程為
的方程為![]() .由
.由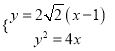 ,得
,得![]() ,從而
,從而![]() . 所以
. 所以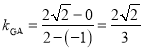 ,
, 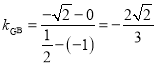 ,所以
,所以![]() ,從而
,從而![]() ,這表明點
,這表明點![]() 到直線
到直線![]() ,
, ![]() 的距離相等,即可證明結果.
的距離相等,即可證明結果.
解法二:(Ⅱ)同解法一可得,直線![]() 的方程為
的方程為![]() ,
,
從而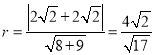 .又直線
.又直線![]() 的方程為
的方程為![]() ,所以點
,所以點![]() 到直線
到直線![]() 的距離
的距離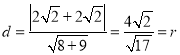 ,即可證明結果.
,即可證明結果.
試題解析:解法一:(Ⅰ)由拋物線的定義得![]() .
.
因為![]() ,即
,即![]() ,解得
,解得![]() ,所以拋物線
,所以拋物線![]() 的方程為
的方程為![]() .
.
(Ⅱ)因為點![]() 在拋物線
在拋物線![]()
![]() 上,
上,
所以![]() ,由拋物線的對稱性,不妨設
,由拋物線的對稱性,不妨設![]() .
.
由![]() ,
, ![]() 可得直線
可得直線![]() 的方程為
的方程為![]() .
.
由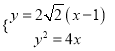 ,得
,得![]() ,
,
解得![]() 或
或![]() ,從而
,從而![]() .
.
又![]() ,
,
所以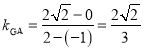 ,
,  ,
,
所以![]() ,從而
,從而![]() ,這表明點
,這表明點![]() 到直線
到直線![]() ,
, ![]() 的距離相等,
的距離相等,
故以![]() 為圓心且與直線
為圓心且與直線![]() 相切的圓必與直線
相切的圓必與直線![]() 相切.
相切.
解法二:(Ⅰ)同解法一.
(Ⅱ)設以點![]() 為圓心且與直線
為圓心且與直線![]() 相切的圓的半徑為
相切的圓的半徑為![]() .
.
因為點![]() 在拋物線
在拋物線![]()
![]() 上,
上,
所以![]() ,由拋物線的對稱性,不妨設
,由拋物線的對稱性,不妨設![]() .
.
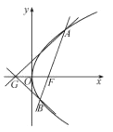
由![]() ,
, ![]() 可得直線
可得直線![]() 的方程為
的方程為![]() .
.
由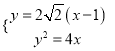 ,得
,得![]() ,
,
解得![]() 或
或![]() ,從而
,從而![]() .
.
又![]() ,故直線
,故直線![]() 的方程為
的方程為![]() ,
,
從而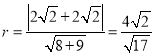 .
.
又直線![]() 的方程為
的方程為![]() ,
,
所以點![]() 到直線
到直線![]() 的距離
的距離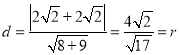 .
.
這表明以點![]() 為圓心且與直線
為圓心且與直線![]() 相切的圓必與直線
相切的圓必與直線![]() 相切.
相切.


科目:高中數學 來源: 題型:
【題目】已知點![]() 為圓
為圓![]() 上一動點,
上一動點,![]() 軸于點
軸于點![]() ,若動點
,若動點![]() 滿足
滿足![]() (其中
(其中![]() 為非零常數)
為非零常數)
(1)求動點![]() 的軌跡方程;
的軌跡方程;
(2)當![]() 時,得到動點
時,得到動點![]() 的軌跡為曲線
的軌跡為曲線![]() ,斜率為
,斜率為![]() 1的直線
1的直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,求
兩點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果不等式ax2+bx+c>0的解集為{x|﹣2<x<4},那么對于函數f(x)=ax2+bx+c應有( )
A.f(5)<f(2)<f(﹣1)
B.f(﹣1)<f(5)<f(2)
C.f(2)<f(﹣1)<f(5)
D.f(5)<f(﹣1)<f(2)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場在一部向下運行的手扶電梯終點的正上方豎直懸掛一幅廣告畫.如圖,該電梯的高AB為4米,它所占水平地面的長AC為8米.該廣告畫最高點E到地面的距離為10.5米.最低點D到地面的距離6.5米.假設某人的眼睛到腳底的距離MN為1.5米,他豎直站在此電梯上觀看DE的視角為θ. 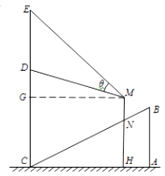
(1)設此人到直線EC的距離為x米,試用x表示點M到地面的距離;
(2)此人到直線EC的距離為多少米,視角θ最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2014年7月16日,中國互聯網絡信息中心發布《第三十四次中國互聯網發展狀況報告》,報告顯示:我國網絡購物用戶已達![]() 億.為了了解網購者一次性購物金額情況,某統計部門隨機抽查了6月1日這一天100名網購者的網購情況,得到如下數據統計表.已知網購金額在2000元以上(不含2000元)的頻率為
億.為了了解網購者一次性購物金額情況,某統計部門隨機抽查了6月1日這一天100名網購者的網購情況,得到如下數據統計表.已知網購金額在2000元以上(不含2000元)的頻率為![]() .
.

(Ⅰ)確定![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)為進一步了解網購金額的多少是否與網齡有關,對這100名網購者調查顯示:購物金額在2000元以上的網購者中網齡3年以上的有35人,購物金額在2000元以下(含2000元)的網購者中網齡不足3年的有20人.
①請將列聯表補充完整;
網齡3年以上 | 網齡不足3年 | 合計 | |
購物金額在2000元以上 | 35 | ||
購物金額在2000元以下 | 20 | ||
合計 | 100 |
②并據此列聯表判斷,是否有![]() %的把握認為網購金額超過2000元與網齡在三年以上有關?
%的把握認為網購金額超過2000元與網齡在三年以上有關?
參考數據:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(參考公式:  ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知正方形ABCD的邊長為6,點E,F分別在邊AB,AD上,AE=AF=4,現將△AEF沿線段EF折起到△A′EF位置,使得A′C=2 ![]() .
. 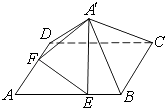
(1)求五棱錐A′﹣BCDFE的體積;
(2)求平面A′EF與平面A′BC的夾角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某品牌汽車4s店對最近100位采用分期付款的購車者進行統計,統計結果如表所示:
付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
頻數 | 40 | 20 | a | 10 | b |
已知分3期付款的頻率為0.2,4s店經銷一輛該品牌的汽車,顧客分1期付款,其利潤為1萬元,分2期或3期付款其利潤為1.5萬元,分4期或5期付款,其利潤為2萬元,用Y表示經銷一輛汽車的利潤.
(1)求上表中a,b的值.
(2)若以頻率作為概率,求事件A:“購買該品牌汽車的3位顧客中,至多有一位采用3期付款”的概率P(A)
(3)求Y的分布列及數學期望EY.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人投籃命中的概率為別為 ![]() 與
與 ![]() ,各自相互獨立,現兩人做投籃游戲,共比賽3局,每局每人各投一球.
,各自相互獨立,現兩人做投籃游戲,共比賽3局,每局每人各投一球.
(1)求比賽結束后甲的進球數比乙的進球數多1個的概率;
(2)設ξ表示比賽結束后,甲、乙兩人進球數的差的絕對值,求ξ的概率分布和數學期望E(ξ).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com