
【題目】已知函數(shù)![]() ,過點(diǎn)
,過點(diǎn)![]() 作與
作與![]() 軸平行的直線交函數(shù)
軸平行的直線交函數(shù)![]() 的圖像于點(diǎn)
的圖像于點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 圖像的切線交
圖像的切線交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,則
,則![]() 面積的最小值為____.
面積的最小值為____.
【答案】![]()
【解析】
求出f(x)的導(dǎo)數(shù),令x=a,求得P的坐標(biāo),可得切線的斜率,運(yùn)用點(diǎn)斜式方程可得切線的方程,令y=0,可得B的坐標(biāo),再由三角形的面積公式可得△ABP面積S,求出導(dǎo)數(shù),利用導(dǎo)數(shù)求最值,即可得到所求值.
函數(shù)f(x)=![]() 的導(dǎo)數(shù)為f′(x)
的導(dǎo)數(shù)為f′(x)![]() ,
,
由題意可令x=a,解得y![]() ,
,
可得P(a,![]() ),
),
即有切線的斜率為k![]() ,
,
切線的方程為y﹣![]() (x
(x![]() ),
),
令y=0,可得x=a﹣1,
即B( a﹣1,0),
在直角三角形PAB中,|AB|=1,|AP|![]() ,
,
則△ABP面積為S(a)![]() |AB||AP|
|AB||AP|![]()
![]() ,a>0,
,a>0,
導(dǎo)數(shù)S′(a)![]()
![]() ,
,
當(dāng)a>1時(shí),S′>0,S(a)遞增;當(dāng)0<a<1時(shí),S′<0,S(a)遞減.
即有a=1處S取得極小值,且為最小值![]() e.
e.
故答案為:![]() e.
e.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】《中國詩詞大會(huì)》(第二季)亮點(diǎn)頗多,十場(chǎng)比賽每場(chǎng)都有一首特別設(shè)計(jì)的開場(chǎng)詩詞,在聲光舞美的配合下,百人團(tuán)齊聲朗誦,別有韻味.若《將進(jìn)酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另確定的兩首詩詞排在后六場(chǎng),且《將進(jìn)酒》排在《望岳》的前面,《山居秋暝》與《送杜少府之任蜀州》不相鄰且均不排在最后,則后六場(chǎng)的排法有( )
A. ![]() 種 B.
種 B. ![]() 種 C.
種 C. ![]() 種 D.
種 D. ![]() 種
種
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
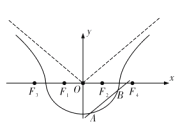
【題目】如圖,曲線![]() 由曲線
由曲線![]() 和曲線
和曲線![]() 組成,其中點(diǎn)
組成,其中點(diǎn)![]() 為曲線
為曲線![]() 所在圓錐曲線的焦點(diǎn),點(diǎn)
所在圓錐曲線的焦點(diǎn),點(diǎn)![]() 為曲線
為曲線![]() 所在圓錐曲線的焦點(diǎn).
所在圓錐曲線的焦點(diǎn).
(Ⅰ)若![]() ,求曲線
,求曲線![]() 的方程;
的方程;
(Ⅱ)如圖,作直線![]() 平行于曲線
平行于曲線![]() 的漸近線,交曲線于點(diǎn)
的漸近線,交曲線于點(diǎn)![]() ,求證:弦
,求證:弦![]() 的中點(diǎn)
的中點(diǎn)![]() 必在曲線
必在曲線![]() 的另一條漸進(jìn)線上;
的另一條漸進(jìn)線上;
(Ⅲ)對(duì)于(Ⅰ)中的曲線![]() ,若直線
,若直線![]() 過點(diǎn)
過點(diǎn)![]() 交曲線
交曲線![]() 于點(diǎn)
于點(diǎn)![]() ,求
,求![]() 與
與![]() 面積之和的最大值.
面積之和的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某廠家舉行大型的促銷活動(dòng),經(jīng)測(cè)算,當(dāng)某產(chǎn)品促銷費(fèi)用為x(萬元)時(shí),銷售量t(萬件)滿足![]() (其中
(其中![]() ,
,![]() ).現(xiàn)假定產(chǎn)量與銷售量相等,已知生產(chǎn)該產(chǎn)品t萬件還需投入成本
).現(xiàn)假定產(chǎn)量與銷售量相等,已知生產(chǎn)該產(chǎn)品t萬件還需投入成本![]() 萬元(不含促銷費(fèi)用),產(chǎn)品的銷售價(jià)格定為
萬元(不含促銷費(fèi)用),產(chǎn)品的銷售價(jià)格定為![]() 元/件.
元/件.
(1)將該產(chǎn)品的利潤y(萬元)表示為促銷費(fèi)用x(萬元)的函數(shù);
(2)促銷費(fèi)用投入多少萬元時(shí),廠家的利潤最大.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(1)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的最大值;
的最大值;
(2)設(shè)![]() ,求函數(shù)
,求函數(shù)![]() 的最大值;
的最大值;
(3)已知![]() ,求函數(shù)
,求函數(shù)![]() 的最大值;
的最大值;
(4)設(shè)![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(I)若![]() 在
在![]() 處取得極值,求過點(diǎn)
處取得極值,求過點(diǎn)![]() 且與
且與![]() 在
在![]() 處的切線平行的直線方程;
處的切線平行的直線方程;
(II)當(dāng)函數(shù)![]() 有兩個(gè)極值點(diǎn)
有兩個(gè)極值點(diǎn)![]() ,且
,且![]() 時(shí),總有
時(shí),總有![]() 成立,求實(shí)數(shù)
成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線 (
(![]() 為參數(shù)),曲線
為參數(shù)),曲線![]() (
(![]() 為參數(shù)).
為參數(shù)).
(1)設(shè)![]() 與
與![]() 相交于
相交于![]() 兩點(diǎn),求
兩點(diǎn),求![]() ;
;
(2)若把曲線![]() 上各點(diǎn)的橫坐標(biāo)壓縮為原來的
上各點(diǎn)的橫坐標(biāo)壓縮為原來的![]() 倍,縱坐標(biāo)壓縮為原來的
倍,縱坐標(biāo)壓縮為原來的![]() 倍,得到曲線
倍,得到曲線![]() ,設(shè)點(diǎn)
,設(shè)點(diǎn)![]() 是曲線
是曲線![]() 上的一個(gè)動(dòng)點(diǎn),求它到直線
上的一個(gè)動(dòng)點(diǎn),求它到直線![]() 的距離的最大時(shí),點(diǎn)P的坐標(biāo).
的距離的最大時(shí),點(diǎn)P的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 且
且![]() ,函數(shù)
,函數(shù)![]() ,
,![]() .
.
(1)指出![]() 的單調(diào)性(不要求證明);
的單調(diào)性(不要求證明);
(2)若有![]() 求
求![]() 的值;
的值;
(3)若![]() ,求使不等式
,求使不等式![]() 恒成立的
恒成立的![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】就實(shí)數(shù)![]() 的取值范圍,討論關(guān)于
的取值范圍,討論關(guān)于![]() 的函數(shù)
的函數(shù)![]() 與
與![]() 軸的交點(diǎn)個(gè)數(shù).
軸的交點(diǎn)個(gè)數(shù).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com