
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 且
且![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)當(dāng)![]() 時(shí),若函數(shù)
時(shí),若函數(shù)![]() 的兩個極值點(diǎn)分別為
的兩個極值點(diǎn)分別為![]() 、
、![]() ,證明
,證明![]() .
.
【答案】(1)![]() 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為![]() ,;無單調(diào)遞減區(qū)間;(2)證明見解析.
,;無單調(diào)遞減區(qū)間;(2)證明見解析.
【解析】
(1)求得![]() ,分類討論,即可求解
,分類討論,即可求解![]() 的單調(diào)區(qū)間,得到答案;
的單調(diào)區(qū)間,得到答案;
(2)根據(jù)![]() 是函數(shù)
是函數(shù)![]() 的兩個零點(diǎn),設(shè)
的兩個零點(diǎn),設(shè)![]() 是方程
是方程![]() 的兩個實(shí)數(shù)解,再根據(jù)二次函數(shù)的性質(zhì)函數(shù)
的兩個實(shí)數(shù)解,再根據(jù)二次函數(shù)的性質(zhì)函數(shù)![]() 在
在![]() 處取得極大值,在
處取得極大值,在![]() 處取得極小值,進(jìn)而得到
處取得極小值,進(jìn)而得到![]() ,代入得
,代入得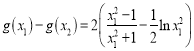 ,令
,令![]() ,則
,則![]() ,得到
,得到![]() ,設(shè)
,設(shè)![]() ,利用導(dǎo)數(shù)求得函數(shù)的單調(diào)性與最值,即可求解.
,利用導(dǎo)數(shù)求得函數(shù)的單調(diào)性與最值,即可求解.
(1)由題意,當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() ,
,
①當(dāng)![]() 時(shí),
時(shí),![]() 恒成立,所以函數(shù)
恒成立,所以函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞增;
上單調(diào)遞增;
②當(dāng)![]() 時(shí),記
時(shí),記![]() ,則
,則![]() ,
,
所以當(dāng)![]() 時(shí),
時(shí),![]() ,∴
,∴![]() 單調(diào)遞減,且
單調(diào)遞減,且![]() ;
;
當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 單調(diào)遞增,且
單調(diào)遞增,且![]() ,
,
所以當(dāng)![]() 時(shí),
時(shí),![]() ,函數(shù)
,函數(shù)![]() 單調(diào)遞增.
單調(diào)遞增.
綜上所述,函數(shù)![]() 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為![]() ,
,![]() ;無單調(diào)遞減區(qū)間.
;無單調(diào)遞減區(qū)間.
(2)由![]() ,
,
![]() ,
,
![]() 是函數(shù)
是函數(shù)![]() 的兩個零點(diǎn),
的兩個零點(diǎn),
![]() 是方程
是方程![]() 的兩個實(shí)數(shù)解,
的兩個實(shí)數(shù)解,
由![]() ,且
,且![]() ,得
,得![]() ,則有
,則有![]() ,
,
不妨設(shè)![]() ,
,![]()
又![]() ,即得
,即得![]() ,
,
![]() ,
,![]() ,
,
即得![]() ,從而得到
,從而得到![]() ,
,
![]() ,且
,且![]() ,
,
![]() 由二次函數(shù)的圖象及性質(zhì)知函數(shù)
由二次函數(shù)的圖象及性質(zhì)知函數(shù)![]() 在
在![]() 處取得極大值,在
處取得極大值,在![]() 處取得極小值.
處取得極小值.
![]()

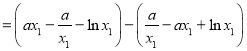
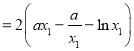 , (*)
, (*)
又![]() 為方程
為方程![]() 的根,
的根,![]() ,
,
代人(*)式得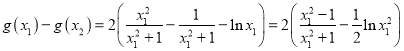 ,
,
令![]() ,則
,則![]() ,
,![]() ,
,
設(shè)![]() ,
,![]() ,
,![]() ,
,![]() 單調(diào)遞減,
單調(diào)遞減,
從而有![]() ,
,![]() .
.
![]() ,即
,即![]() 得證.
得證.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,已知
中,已知![]() 分別為橢圓
分別為橢圓![]() 的左、右焦點(diǎn),且橢圓經(jīng)過點(diǎn)
的左、右焦點(diǎn),且橢圓經(jīng)過點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() ,其中
,其中![]() 為橢圓的離心率.
為橢圓的離心率.

(1)求橢圓的方程;
(2)過點(diǎn)![]() 的直線
的直線![]() 橢圓于另一點(diǎn)
橢圓于另一點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 在直線
在直線![]() 上,且
上,且![]() .若
.若![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線![]() 與橢圓
與橢圓![]() 切于點(diǎn)
切于點(diǎn)![]() ,與圓
,與圓![]() 交于點(diǎn)
交于點(diǎn)![]() ,圓
,圓![]() 在點(diǎn)
在點(diǎn)![]() 處的切線交于點(diǎn)
處的切線交于點(diǎn)![]() ,
,![]() 為坐標(biāo)原點(diǎn),則
為坐標(biāo)原點(diǎn),則![]() 的面積的最大值為( )
的面積的最大值為( )
A.![]() B.2C.
B.2C.![]() D.1
D.1
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市政府為減輕汽車尾氣對大氣的污染,保衛(wèi)藍(lán)天,鼓勵廣大市民使用電動交通工具出行,決定為電動車(含電動自行車和電動汽車)免費(fèi)提供電池檢測服務(wù).現(xiàn)從全市已掛牌照的![]() 電動車中隨機(jī)抽取100輛委托專業(yè)機(jī)構(gòu)免費(fèi)為它們進(jìn)行電池性能檢測,電池性能分為需要更換、尚能使用、較好、良好四個等級,并分成電動自行車和電動汽車兩個群體分別進(jìn)行統(tǒng)計(jì),樣本分布如圖.
電動車中隨機(jī)抽取100輛委托專業(yè)機(jī)構(gòu)免費(fèi)為它們進(jìn)行電池性能檢測,電池性能分為需要更換、尚能使用、較好、良好四個等級,并分成電動自行車和電動汽車兩個群體分別進(jìn)行統(tǒng)計(jì),樣本分布如圖.
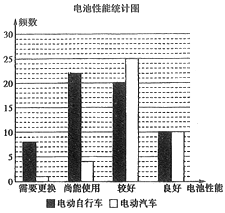
(1)采用分層抽樣的方法從電池性能較好的電動車中隨機(jī)抽取9輛,再從這9輛中隨機(jī)抽取2輛,求至少有一輛為電動汽車的概率;
(2)為進(jìn)一步提高市民對電動車的使用熱情,市政府準(zhǔn)備為電動車車主一次性發(fā)放補(bǔ)助,標(biāo)準(zhǔn)如下:①電動自行車每輛補(bǔ)助300元;②電動汽車每輛補(bǔ)助500元;③對電池需要更換的電動車每輛額外補(bǔ)助400元.試求抽取的100輛電動車執(zhí)行此方案的預(yù)算;并利用樣本估計(jì)總體,試估計(jì)市政府執(zhí)行此方案的預(yù)算.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地的中小學(xué)辦學(xué)條件在政府的教育督導(dǎo)下,迅速得到改變.教育督導(dǎo)一年后.分別隨機(jī)抽查了初中(用![]() 表示)與小學(xué)(用
表示)與小學(xué)(用![]() 表示)各10所學(xué)校.得到相關(guān)指標(biāo)的綜合評價(jià)得分(百分制)的莖葉圖如圖所示.則從莖葉圖可得出正確的信息為( )(80分及以上為優(yōu)秀). ①初中得分與小學(xué)得分的優(yōu)秀率相同;②初中得分與小學(xué)得分的中位數(shù)相同③初中得分的方差比小學(xué)得分的方差大④初中得分與小學(xué)得分的平均分相同.
表示)各10所學(xué)校.得到相關(guān)指標(biāo)的綜合評價(jià)得分(百分制)的莖葉圖如圖所示.則從莖葉圖可得出正確的信息為( )(80分及以上為優(yōu)秀). ①初中得分與小學(xué)得分的優(yōu)秀率相同;②初中得分與小學(xué)得分的中位數(shù)相同③初中得分的方差比小學(xué)得分的方差大④初中得分與小學(xué)得分的平均分相同.

A.①②B.①③C.②④D.③④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(Ⅰ)記![]() ,試判斷函數(shù)
,試判斷函數(shù)![]() 的極值點(diǎn)的情況;
的極值點(diǎn)的情況;
(Ⅱ)若![]() 有且僅有兩個整數(shù)解,求實(shí)數(shù)
有且僅有兩個整數(shù)解,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四棱錐P-ABCD的底面ABCD是矩形,PA⊥平面ABCD, PA=AD=2,E,F分別為PA,AB的中點(diǎn),且DF⊥CE.
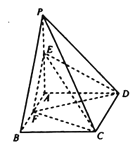
(1)求AB的長;
(2)求直線CF與平面DEF所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 的最小值為
的最小值為![]() ,
,![]() 的圖象的相鄰兩條對稱軸之間的距離為
的圖象的相鄰兩條對稱軸之間的距離為![]() ,
,![]() 的圖象關(guān)于原點(diǎn)對稱.
的圖象關(guān)于原點(diǎn)對稱.
(1)求函數(shù)![]() 的解析式和單調(diào)遞增區(qū)間;
的解析式和單調(diào)遞增區(qū)間;
(2)在![]() 中,角
中,角![]() 所對的邊分別為
所對的邊分別為![]() ,且
,且![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,三棱錐![]() 中,
中,![]() 底面
底面![]() 為等邊三角形,
為等邊三角形,![]() 分別是
分別是![]() 的中點(diǎn).
的中點(diǎn).
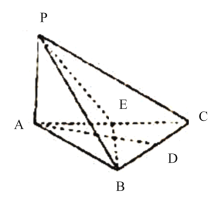
(1)證明:平面![]() 平面
平面![]() ;
;
(2)如何在![]() 上找一點(diǎn)
上找一點(diǎn)![]() ,使
,使![]() 平面
平面![]() 并說明理由;
并說明理由;
(3)若![]() ,對于(2)中的點(diǎn)
,對于(2)中的點(diǎn)![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com