
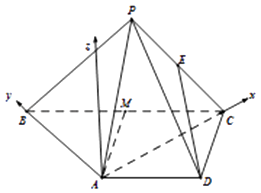
【題目】在四棱錐P﹣ABCD中,AD∥BC,AD=AB=DC= ![]() BC=1,E是PC的中點,面PAC⊥面ABCD.
BC=1,E是PC的中點,面PAC⊥面ABCD.
(Ⅰ)證明:ED∥面PAB;
(Ⅱ)若PC=2,PA= ![]() ,求二面角A﹣PC﹣D的余弦值.
,求二面角A﹣PC﹣D的余弦值.
【答案】(Ⅰ)證明:取PB的中點F,連接AF,EF.
∵EF是△PBC的中位線,∴EF∥BC,且EF= ![]() .
.
又AD=BC,且AD= ![]() ,∴AD∥EF且AD=EF,
,∴AD∥EF且AD=EF,
則四邊形ADEF是平行四邊形.
∴DE∥AF,又DE面ABP,AF面ABP,
∴ED∥面PAB;
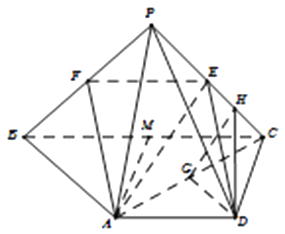
(Ⅱ)解:法一、取BC的中點M,連接AM,則AD∥MC且AD=MC,
∴四邊形ADCM是平行四邊形,
∴AM=MC=MB,則A在以BC為直徑的圓上.
∴AB⊥AC,可得 ![]() .
.
過D作DG⊥AC于G,
∵平面PAC⊥平面ABCD,且平面PAC∩平面ABCD=AC,
∴DG⊥平面PAC,則DG⊥PC.
過G作GH⊥PC于H,則PC⊥面GHD,連接DH,則PC⊥DH,
∴∠GHD是二面角A﹣PC﹣D的平面角.
在△ADC中, ![]() ,連接AE,
,連接AE, ![]() .
.
在Rt△GDH中, ![]() ,
,
∴ ![]() ,
,
即二面角A﹣PC﹣D的余弦值 ![]() .
.
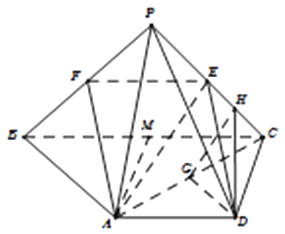
法二、取BC的中點M,連接AM,則AD∥MC,且AD=MC.
∴四邊形ADCM是平行四邊形,
∴AM=MC=MB,則A在以BC為直徑的圓上,
∴AB⊥AC.
∵面PAC⊥平面ABCD,且平面PAC∩平面ABCD=AC,∴AB⊥面PAC.
如圖以A為原點, ![]() 方向分別為x軸正方向,y軸正方向建立空間直角坐標系.
方向分別為x軸正方向,y軸正方向建立空間直角坐標系.
可得 ![]() ,
, 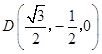 .
.
設P(x,0,z),(z>0),依題意有 ![]() ,
, ![]() ,
,
解得 ![]() .
.
則 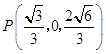 ,
, 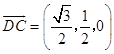 ,
, 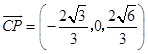 .
.
設面PDC的一個法向量為 ![]() ,
,
由 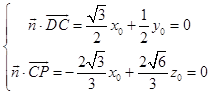 ,取x0=1,得
,取x0=1,得 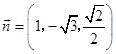 .
.
![]() 為面PAC的一個法向量,且
為面PAC的一個法向量,且 ![]() ,
,
設二面角A﹣PC﹣D的大小為θ,
則有 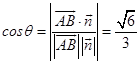 ,即二面角A﹣PC﹣D的余弦值
,即二面角A﹣PC﹣D的余弦值 ![]() .
.
【解析】
【考點精析】利用直線與平面平行的判定對題目進行判斷即可得到答案,需要熟知平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行.


 巧學巧練系列答案
巧學巧練系列答案科目:高中數學 來源: 題型:
【題目】若函數y=f(x)在R上可導且滿足不等式xf′(x)+f(x)>0恒成立,且常數a,b滿足a>b,則下列不等式一定成立的是( )
A.af(a)>bf(b)
B.af(b)>bf(a)
C.af(a)<bf(b)
D.af(b)<bf(a)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數y=ksin(kx+φ)( ![]() )與函數y=kx﹣k2+6的部分圖象如圖所示,則函數f(x)=sin(kx﹣φ)+cos(kx﹣φ)圖象的一條對稱軸的方程可以為( )
)與函數y=kx﹣k2+6的部分圖象如圖所示,則函數f(x)=sin(kx﹣φ)+cos(kx﹣φ)圖象的一條對稱軸的方程可以為( ) 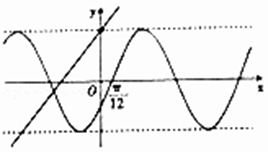
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某沿海四個城市A,B,C,D的位置如圖所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30 ![]() nmile,AD=70
nmile,AD=70 ![]() nmile,D位于A的北偏東75°方向.現在有一艘輪船從A出發向直線航行,一段時間到達D后,輪船收到指令改向城市C直線航行,收到指令時城市C對于輪船的方位角是南偏西θ度,則sinθ= .
nmile,D位于A的北偏東75°方向.現在有一艘輪船從A出發向直線航行,一段時間到達D后,輪船收到指令改向城市C直線航行,收到指令時城市C對于輪船的方位角是南偏西θ度,則sinθ= . 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某四棱錐的三視圖如圖所示,俯視圖是一個等腰直角三角形,則該四棱錐的表面積是( ) 
A.2 ![]() +2
+2 ![]() +2
+2
B.3 ![]() +2
+2 ![]() +3
+3
C.2 ![]() +
+ ![]() +2
+2
D.3 ![]() +
+ ![]() +3
+3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an},{bn}滿足:bn=an+1﹣an(n∈N*).
(1)若a1=1,bn=n,求數列{an}的通項公式;
(2)若bn+1bn﹣1=bn(n≥2),且b1=1,b2=2. (i)記cn=a6n﹣1(n≥1),求證:數列{cn}為等差數列;
(ii)若數列{ ![]() }中任意一項的值均未在該數列中重復出現無數次,求首項a1應滿足的條件.
}中任意一項的值均未在該數列中重復出現無數次,求首項a1應滿足的條件.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣ax(a>0),設 ![]() .
.
(1)判斷函數h(x)=f(x)﹣g(x)零點的個數,并給出證明;
(2)首項為m的數列{an}滿足:①an+1+an≠ ![]() ;②f(an+1)=g(an).其中0<m<
;②f(an+1)=g(an).其中0<m< ![]() .求證:對于任意的i,j∈N* , 均有ai﹣aj<
.求證:對于任意的i,j∈N* , 均有ai﹣aj< ![]() ﹣m.
﹣m.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓C: ![]() 過點P(
過點P( ![]() ,1)且離心率為
,1)且離心率為 ![]() ,F為橢圓的右焦點,過F的直線交橢圓C于M,N兩點,定點A(﹣4,0).
,F為橢圓的右焦點,過F的直線交橢圓C于M,N兩點,定點A(﹣4,0).
(Ⅰ)求橢圓C的方程;
(Ⅱ)若△AMN面積為3 ![]() ,求直線MN的方程.
,求直線MN的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com