
【題目】已知橢圓:![]() 的離心率為
的離心率為![]() ,圓
,圓![]() 的圓心與橢圓C的上頂點(diǎn)重合,點(diǎn)P的縱坐標(biāo)為
的圓心與橢圓C的上頂點(diǎn)重合,點(diǎn)P的縱坐標(biāo)為![]() .
.
(1)求橢圓C的標(biāo)準(zhǔn)方程;
(2)若斜率為2的直線l與橢圓C交于A,B兩點(diǎn),探究:在橢圓C上是否存在一點(diǎn)Q,使得![]() ,若存在,求出點(diǎn)Q的坐標(biāo);若不存在,請(qǐng)說明理由.
,若存在,求出點(diǎn)Q的坐標(biāo);若不存在,請(qǐng)說明理由.
【答案】(1)![]() ;(2)不存在.
;(2)不存在.
【解析】
(2)求出圓心的坐標(biāo),得到![]() .結(jié)合橢圓的離心率及
.結(jié)合橢圓的離心率及![]() 列方程組,解方程組求得
列方程組,解方程組求得![]() 的值,進(jìn)而求得橢圓的標(biāo)準(zhǔn)方程.(2)首先假設(shè)存在這樣的
的值,進(jìn)而求得橢圓的標(biāo)準(zhǔn)方程.(2)首先假設(shè)存在這樣的![]() 點(diǎn),設(shè)出
點(diǎn),設(shè)出![]() 的坐標(biāo)以及直線
的坐標(biāo)以及直線![]() 的方程,得到
的方程,得到![]() 兩點(diǎn)的坐標(biāo),代入
兩點(diǎn)的坐標(biāo),代入![]() ,聯(lián)立直線
,聯(lián)立直線![]() 的方程和橢圓方程,求得判別式.將
的方程和橢圓方程,求得判別式.將![]() 點(diǎn)坐標(biāo)代入橢圓方程,同樣求其判別式.兩次求得的判別式?jīng)]有交集,故不存在這樣的
點(diǎn)坐標(biāo)代入橢圓方程,同樣求其判別式.兩次求得的判別式?jīng)]有交集,故不存在這樣的![]() 點(diǎn).
點(diǎn).
(1)由橢圓的離心率![]() ,則
,則![]() ,b2=a2﹣c2=c2,
,b2=a2﹣c2=c2,
由x2+y2﹣2y=0的標(biāo)準(zhǔn)方程x2+(y﹣1)2=1,則b=1,c=1,a=![]() ,
,
∴橢圓的標(biāo)準(zhǔn)方程:![]() ;
;
(2)假設(shè)存在Q,使得滿足![]() ,
,
設(shè)A(x1,y1),B(x2,y2).直線l:y=2x+m,
則Q(x0,y0),P(p,![]() ),則
),則![]() =(x1﹣p,y1﹣
=(x1﹣p,y1﹣![]() ),
),![]() =(x0﹣x2,y0﹣y2),
=(x0﹣x2,y0﹣y2),
由![]() ,則
,則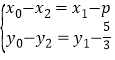 ,
,
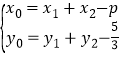 ,則
,則![]() ,整理得:9x2+8mx+2m2﹣2=0,
,整理得:9x2+8mx+2m2﹣2=0,
則△=(8m)2﹣4×9×(2m2﹣2)=8(9﹣m2)>0,解得:﹣3<m<3,①
則x1+x2=﹣![]() m,y1+y2=2(x1+x2)+2m=
m,y1+y2=2(x1+x2)+2m=![]() m, 則x0=﹣
m, 則x0=﹣![]() m﹣p,y0=
m﹣p,y0=![]() m﹣
m﹣![]() ,
,
由Q(x0,y0)在橢圓上,則x02+2y02=2,
∴(﹣![]() m﹣p)2+2(
m﹣p)2+2(![]() m﹣
m﹣![]() )2=2,整理得:9p2+16mp+8m2﹣
)2=2,整理得:9p2+16mp+8m2﹣![]() m+32=0有解,
m+32=0有解,
則△2=(16m)2﹣4×9(8m2﹣![]() m+32)=648﹣32(m﹣
m+32)=648﹣32(m﹣![]() )2≥0,
)2≥0,
解得:3≤m≤12,② ①②無交集,因此不存在Q,使得![]() .
.


 精英口算卡系列答案
精英口算卡系列答案 應(yīng)用題點(diǎn)撥系列答案
應(yīng)用題點(diǎn)撥系列答案 狀元及第系列答案
狀元及第系列答案 同步奧數(shù)系列答案
同步奧數(shù)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】每年10月中上旬是小麥的最佳種植時(shí)間,但小麥的發(fā)芽會(huì)受到土壤、氣候等多方面因素的影響.某科技小組為了解晝夜溫差的大小與小麥發(fā)芽的多少之間的關(guān)系,在不同的溫差下統(tǒng)計(jì)了100顆小麥種子的發(fā)芽數(shù),得到了如下數(shù)據(jù):
溫差 | 8 | 10 | 11 | 12 | 13 |
發(fā)芽數(shù) | 79 | 81 | 85 | 86 | 90 |
(1)請(qǐng)根據(jù)統(tǒng)計(jì)的最后三組數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若由(1)中的線性回歸方程得到的估計(jì)值與前兩組數(shù)據(jù)的實(shí)際值誤差均不超過兩顆,則認(rèn)為線性回歸方程是可靠的,試判斷(1)中得到的線性回歸方程是否可靠;
(3)若100顆小麥種子的發(fā)芽率為![]() 顆,則記為
顆,則記為![]() 的發(fā)芽率,當(dāng)發(fā)芽率為
的發(fā)芽率,當(dāng)發(fā)芽率為![]() 時(shí),平均每畝地的收益為
時(shí),平均每畝地的收益為![]() 元,某農(nóng)場(chǎng)有土地10萬畝,小麥種植期間晝夜溫差大約為
元,某農(nóng)場(chǎng)有土地10萬畝,小麥種植期間晝夜溫差大約為![]() ,根據(jù)(1)中得到的線性回歸方程估計(jì)該農(nóng)場(chǎng)種植小麥所獲得的收益.
,根據(jù)(1)中得到的線性回歸方程估計(jì)該農(nóng)場(chǎng)種植小麥所獲得的收益.
附:在線性回歸方程![]() 中,
中,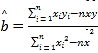 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某保險(xiǎn)公司決定每月給推銷員確定個(gè)具體的銷售目標(biāo),對(duì)推銷員實(shí)行目標(biāo)管理.銷售目標(biāo)確定的適當(dāng)與否,直接影響公司的經(jīng)濟(jì)效益和推銷員的工作積極性,為此,該公司當(dāng)月隨機(jī)抽取了50位推銷員上個(gè)月的月銷售額(單位:萬元),繪制成如圖所示的頻率分布直方圖.

(1)①根據(jù)圖中數(shù)據(jù),求出月銷售額在![]() 小組內(nèi)的頻率.
小組內(nèi)的頻率.
②根據(jù)直方圖估計(jì),月銷售目標(biāo)定為多少萬元時(shí),能夠使70%的推銷員完成任務(wù)?并說明理由.
(2)該公司決定從月銷售額為![]() 和
和![]() 的兩個(gè)小組中,選取2位推銷員介紹銷售經(jīng)驗(yàn),求選出的推銷員來自同一個(gè)小組的概率.
的兩個(gè)小組中,選取2位推銷員介紹銷售經(jīng)驗(yàn),求選出的推銷員來自同一個(gè)小組的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對(duì)于函數(shù)![]() 與
與![]() ,若存在實(shí)數(shù)
,若存在實(shí)數(shù)![]() 滿足
滿足![]() ,且
,且![]() ,則稱
,則稱![]() 為
為![]() 的一個(gè)
的一個(gè)![]() 點(diǎn).
點(diǎn).
(1)證明:函數(shù)![]() 與
與![]() 不存在
不存在![]() 的
的![]() 點(diǎn);
點(diǎn);
(2)若函數(shù)![]() 與
與![]() 存在
存在![]() 的
的![]() 點(diǎn)
點(diǎn)![]() ,求
,求![]() 的范圍;
的范圍;
(3)已知函數(shù)![]() ,證明:存在正實(shí)數(shù)
,證明:存在正實(shí)數(shù)![]() ,對(duì)于區(qū)間
,對(duì)于區(qū)間![]() 內(nèi)任意一個(gè)
內(nèi)任意一個(gè)![]() 皆是函數(shù)
皆是函數(shù)![]() 的
的![]() 點(diǎn).
點(diǎn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一盒中裝有9張各寫有一個(gè)數(shù)字的卡片,其中4張卡片上的數(shù)字是1,3張卡片上的數(shù)字是2,2張卡片上的數(shù)字是3,從盒中任取3張卡片.
(1)求所取3張卡片上的數(shù)字完全相同的概率;
(2)![]() 表示所取3張卡片上的數(shù)字的中位數(shù),求
表示所取3張卡片上的數(shù)字的中位數(shù),求![]() 的分布列與數(shù)學(xué)期望.
的分布列與數(shù)學(xué)期望.
(注:若三個(gè)數(shù)![]() 滿足
滿足![]() ,則稱
,則稱![]() 為這三個(gè)數(shù)的中位數(shù)).
為這三個(gè)數(shù)的中位數(shù)).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)欲做一個(gè)介紹企業(yè)發(fā)展史的銘牌,銘牌的截面形狀是如圖所示的扇形環(huán)面(由扇形![]() 挖去扇形
挖去扇形![]() 后構(gòu)成的).已知
后構(gòu)成的).已知![]() ,線段
,線段![]() 與弧
與弧![]() 、弧
、弧![]() 的長(zhǎng)度之和為
的長(zhǎng)度之和為![]() 米,圓心角為
米,圓心角為![]() 弧度.
弧度.

(1)求![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式;
的函數(shù)解析式;
(2)記銘牌的截面面積為![]() ,試問
,試問![]() 取何值時(shí),
取何值時(shí),![]() 的值最大?并求出最大值.
的值最大?并求出最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() (
(![]() 為參數(shù)),A,B是C上的動(dòng)點(diǎn),且滿足
為參數(shù)),A,B是C上的動(dòng)點(diǎn),且滿足![]() (O為坐標(biāo)原點(diǎn)),以原點(diǎn)O為極點(diǎn),x軸的正半軸為極軸建立坐標(biāo)系,點(diǎn)D的極坐標(biāo)為
(O為坐標(biāo)原點(diǎn)),以原點(diǎn)O為極點(diǎn),x軸的正半軸為極軸建立坐標(biāo)系,點(diǎn)D的極坐標(biāo)為![]() .
.
(1)求橢圓C的極坐標(biāo)方程和點(diǎn)D的直角坐標(biāo);
(2)利用橢圓C的極坐標(biāo)方程證明 為定值.
為定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地區(qū)工會(huì)利用“健步行![]() ”開展明年健步走積分獎(jiǎng)勵(lì)活動(dòng).會(huì)員每天走5千步可獲積分30分(不足5千步不積分),每多走2千步再積20分(不足2千步不積分).為了解會(huì)員的健步走情況,工會(huì)在某天從系統(tǒng)中隨機(jī)抽取了1000名會(huì)員,統(tǒng)計(jì)了當(dāng)天他們的步數(shù),并將樣本數(shù)據(jù)分為
”開展明年健步走積分獎(jiǎng)勵(lì)活動(dòng).會(huì)員每天走5千步可獲積分30分(不足5千步不積分),每多走2千步再積20分(不足2千步不積分).為了解會(huì)員的健步走情況,工會(huì)在某天從系統(tǒng)中隨機(jī)抽取了1000名會(huì)員,統(tǒng)計(jì)了當(dāng)天他們的步數(shù),并將樣本數(shù)據(jù)分為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 九組,整理得到如下頻率分布直方圖:
九組,整理得到如下頻率分布直方圖:
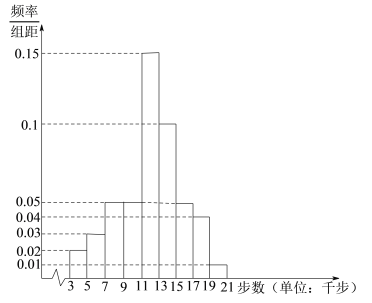
(1)從當(dāng)天步數(shù)在![]() ,
,![]() ,
,![]() 的會(huì)員中按分層抽樣的方式抽取6人,再?gòu)倪@6人中隨機(jī)抽取2人,求這2人積分之和不少于220分的概率;
的會(huì)員中按分層抽樣的方式抽取6人,再?gòu)倪@6人中隨機(jī)抽取2人,求這2人積分之和不少于220分的概率;
(2)求該組數(shù)據(jù)的中位數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖:在四棱錐![]() 中,
中,![]() 平面
平面![]() .
.![]() ,
,![]() ,
,![]() .點(diǎn)
.點(diǎn)![]() 是
是![]() 與
與![]() 的交點(diǎn),點(diǎn)
的交點(diǎn),點(diǎn)![]() 在線段
在線段![]() 上且
上且![]() .
.

(1)證明:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(3)求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com