
【題目】數列![]() 中,
中,![]() ,
,![]() ,數列
,數列![]() 滿足
滿足![]() .
.
(1)求數列![]() 中的前四項;
中的前四項;
(2)求證:數列![]() 是等差數列;
是等差數列;
(3)若![]() ,試判斷數列
,試判斷數列![]() 是否有最小項,若有最小項,求出最小項.
是否有最小項,若有最小項,求出最小項.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】設全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的部分圖象如圖所示:
的部分圖象如圖所示:
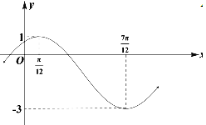
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的單調區間和對稱中心坐標;
的單調區間和對稱中心坐標;
(3)將![]() 的圖象向左平移
的圖象向左平移![]() 個單位,再將橫坐標伸長到原來的2倍,縱坐標不變,最后將圖象向上平移1個單位,得到函數
個單位,再將橫坐標伸長到原來的2倍,縱坐標不變,最后將圖象向上平移1個單位,得到函數![]() 的圖象,求函數
的圖象,求函數![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 滿足
滿足![]() 且
且![]() ,則稱函數
,則稱函數![]() 為“
為“![]() 函數”.
函數”.
![]() 試判斷
試判斷![]() 是否為“
是否為“![]() 函數”,并說明理由;
函數”,并說明理由;
![]() 函數
函數![]() 為“
為“![]() 函數”,且當
函數”,且當![]() 時,
時,![]() ,求
,求![]() 的解析式,并寫出在
的解析式,并寫出在![]() 上的單調遞增區間;
上的單調遞增區間;
![]() 在
在![]() 條件下,當
條件下,當![]() 時,關于
時,關于![]() 的方程
的方程![]() 為常數
為常數![]() 有解,記該方程所有解的和為
有解,記該方程所有解的和為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某測試團隊為了研究“飲酒”對“駕車安全”的影響,隨機選取![]() 名駕駛員先后在無酒狀態、酒后狀態下進行“停車距離”測試.測試的方案:電腦模擬駕駛,以某速度勻速行駛,記錄下駕駛員的“停車距離”(駕駛員從看到意外情況到車子完全停下所需要的距離).無酒狀態與酒后狀態下的試驗數據分別列于表1和表2.
名駕駛員先后在無酒狀態、酒后狀態下進行“停車距離”測試.測試的方案:電腦模擬駕駛,以某速度勻速行駛,記錄下駕駛員的“停車距離”(駕駛員從看到意外情況到車子完全停下所需要的距離).無酒狀態與酒后狀態下的試驗數據分別列于表1和表2.
表1
停車距離 |
|
|
|
|
|
頻數 | 24 | 42 | 24 | 9 | 1 |
表2
平均每毫升血液酒精含量 | 10 | 30 | 50 | 70 | 90 |
平均停車距離 | 30 | 50 | 60 | 70 | 90 |
回答以下問題.
(1)由表1估計駕駛員無酒狀態下停車距離的平均數;
(2)根據最小二乘法,由表2的數據計算![]() 關于
關于![]() 的回歸方程
的回歸方程![]() ;
;
(3)該測試團隊認為:駕駛員酒后駕車的平均“停車距離”![]() 大于(1)中無酒狀態下的停車距離平均數的
大于(1)中無酒狀態下的停車距離平均數的![]() 倍,則認定駕駛員是“醉駕”.請根據(2)中的回歸方程,預測當每毫升血液酒精含量大于多少毫克時為“醉駕”?(精確到個位)
倍,則認定駕駛員是“醉駕”.請根據(2)中的回歸方程,預測當每毫升血液酒精含量大于多少毫克時為“醉駕”?(精確到個位)
(附:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為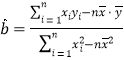 ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 下列結論錯誤的是
A. 命題:“若![]() ,則
,則![]() ”的逆否命題是“若
”的逆否命題是“若![]() ,則
,則![]() ”
”
B. “![]() ”是“
”是“![]() ”的充分不必要條件
”的充分不必要條件
C. 命題:“![]() ,
, ![]() ”的否定是“
”的否定是“![]() ,
, ![]() ”
”
D. 若“![]() ”為假命題,則
”為假命題,則![]() 均為假命題
均為假命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是定義在
是定義在![]() 上的奇函數,且
上的奇函數,且![]() ,若
,若![]() 且
且![]() 時,有
時,有![]() 成立.
成立.
(1)判斷![]() 在
在![]() 上的單調性,并用定義證明;
上的單調性,并用定義證明;
(2)解不等式![]() ;
;
(3)若![]() 對所有的
對所有的![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com