
【題目】如圖,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱臺形玻璃容器Ⅱ的高均為32cm,容器Ⅰ的底面對角線AC的長為10![]() cm,容器Ⅱ的兩底面對角線
cm,容器Ⅱ的兩底面對角線![]() ,
,![]() 的長分別為14cm和62cm.分別在容器Ⅰ和容器Ⅱ中注入水,水深均為12cm.現有一根玻璃棒l,其長度為40cm.(容器厚度、玻璃棒粗細均忽略不計)
的長分別為14cm和62cm.分別在容器Ⅰ和容器Ⅱ中注入水,水深均為12cm.現有一根玻璃棒l,其長度為40cm.(容器厚度、玻璃棒粗細均忽略不計)
(1)將![]() 放在容器Ⅰ中,
放在容器Ⅰ中,![]() 的一端置于點A處,另一端置于側棱
的一端置于點A處,另一端置于側棱![]() 上,求
上,求![]() 沒入水中部分的長度;
沒入水中部分的長度;
(2)將![]() 放在容器Ⅱ中,
放在容器Ⅱ中,![]() 的一端置于點E處,另一端置于側棱
的一端置于點E處,另一端置于側棱![]() 上,求
上,求![]() 沒入水中部分的長度.
沒入水中部分的長度.
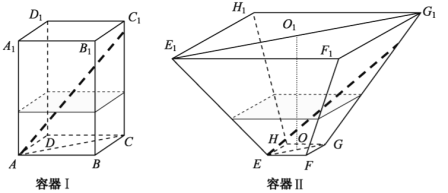
【答案】(1)16;(2)20.
【思路分析】(1)轉化為直角三角形ACM中,利用相似性質求解AP1;(2)轉化到三角形EGN中,先利用直角梯形性質求角![]() ,再利用正弦定理求角
,再利用正弦定理求角![]() ,最后根據直角三角形求高,即為
,最后根據直角三角形求高,即為![]() 沒入水中部分的長度.
沒入水中部分的長度.
【解析】(1)由正棱柱的定義,![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,![]() .
.
記玻璃棒的另一端落在![]() 上點
上點![]() 處.
處.
因為![]() ,所以
,所以![]() ,從而
,從而![]() ,
,
如圖,![]() 與水面的交點為
與水面的交點為![]() ,過
,過![]() 作P1Q1⊥AC,Q1為垂足,
作P1Q1⊥AC,Q1為垂足,

則P1Q1⊥平面ABCD,故P1Q1=12,從而AP1=![]() .
.
答:玻璃棒l沒入水中部分的長度為16cm.
(如果將“沒入水中部分”理解為“水面以上部分”,則結果為24cm)
(2)如圖,O,O1是正棱臺的兩底面中心.

由正棱臺的定義,OO1⊥平面EFGH,所以平面E1EGG1⊥平面EFGH,O1O⊥EG.
同理,平面E1EGG1⊥平面E1F1G1H1,O1O⊥E1G1.
記玻璃棒的另一端落在GG1上點N處.
過G作GK⊥E1G1,K為垂足,則GK =OO1=32.
因為EG = 14,E1G1= 62,
所以KG1=![]() ,從而
,從而![]() .
.
設![]() 則
則![]() .
.
因為![]() ,所以
,所以![]() .
.
在![]() 中,由正弦定理可得
中,由正弦定理可得![]() ,解得
,解得![]() .
.
因為![]() ,所以
,所以![]() .
.
于是![]() .
.
記EN與水面的交點為P2,過P2作P2Q2⊥EG,Q2為垂足,則P2Q2⊥平面EFGH,
故P2Q2=12,從而EP2=![]() .
.
答:玻璃棒l沒入水中部分的長度為20cm.
(如果將“沒入水中部分”理解為“水面以上部分”,則結果為20cm)


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某大學餐飲中心為了解新生的飲食習慣,在全校一年級學生中進行了抽樣調查,調查結果如下表所示:
喜歡甜品 | 不喜歡甜品 | 合 計 | |
南方學生 | 60 | 20 | 80 |
北方學生 | 10 | 10 | 20 |
合 計 | 70 | 30 | 100 |
⑴根據表中數據,問是否有95%的把握認為“南方學生和北方學生在選用甜品的飲食習慣方面有差
異”;
⑵已知在被調查的北方學生中有5名數學系的學生,其中2名喜歡甜品,現在從這5名學生中隨機
抽取3人,求至多有1人喜歡甜品的概率.
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
附: 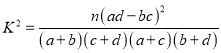 ,
,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修![]() :坐標系與參數方程選講.
:坐標系與參數方程選講.
在平面直角坐標系![]() 中,曲線
中,曲線![]() (
(![]() 為參數,實數
為參數,實數![]() ),曲線
),曲線![]()
![]() (
(![]() 為參數,實數
為參數,實數![]() ). 在以
). 在以![]() 為極點,
為極點, ![]() 軸的正半軸為極軸的極坐標系中,射線
軸的正半軸為極軸的極坐標系中,射線![]() 與
與![]() 交于
交于![]() 兩點,與
兩點,與![]() 交于
交于![]() 兩點. 當
兩點. 當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() .
.
(1)求![]() 的值; (2)求
的值; (2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() ,函數
,函數![]() 的圖象在點
的圖象在點![]() 處的切線平行于
處的切線平行于![]() 軸.
軸.
(1)求![]() 的值;
的值;
(2)求函數![]() 的極小值;
的極小值;
(3)設斜率為![]() 的直線與函數
的直線與函數![]() 的圖象交于兩點
的圖象交于兩點![]() ,
, ![]() ,
, ![]() ,證明:
,證明: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,游客從某旅游景區的景點A處下山至C處有兩種路徑.一種是從A沿直線步行到C,另一種是先從A沿索道乘纜車到B,然后從B沿直線步行到C.
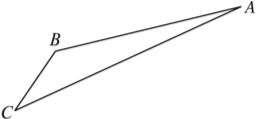
現有甲、乙兩位游客從A處下山,甲沿AC勻速步行,速度為50 m/min,在甲出發2 min后,乙從A乘纜車到B,在B處停留1 min后,再從B勻速步行到C.假設纜車勻速直線運行的速度為130 m/min,山路AC長為1 260 m,經測量,cos A=![]() ,cos C=
,cos C=![]() .
.
(1)求索道AB的長;
(2)問乙出發多少分鐘后,乙在纜車上與甲的距離最短?
(3)為使兩位游客在C處互相等待的時間不超過3分鐘,乙步行的速度應控制在什么范圍內?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據統計,截至2016年底全國微信注冊用戶數量已經突破9.27億.為調查大學生這個微信用戶群體中每人擁有微信群的數量,現從某市大學生中隨機抽取100位同學進行了抽樣調查,結果如下:
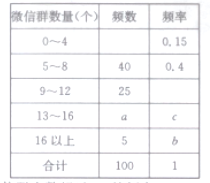
(1)求![]() ,
,![]() ,
,![]() 的值及樣本中微信群個數超過12的概率;
的值及樣本中微信群個數超過12的概率;
(2)若從這100位同學中隨機抽取2人,求這2人中恰有1人微信群個數超過12的概率;
(3)以(1)中的頻率作為概率,若從全市大學生中隨機抽取3人,記![]() 表示抽到的是微信群個數超過12的人數,求
表示抽到的是微信群個數超過12的人數,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017唐山模擬】如圖,ABCDA1B1C1D1為正方體,連接BD,AC1,B1D1, CD1,B1C,現有以下幾個結論:①BD∥平面CB1D1;②AC1⊥平面CB1D1;③AC1與底面ABCD所成角的正切值是;④CB1與BD為異面直線,其中所有正確結論的序號為________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com