
【題目】如圖,四棱錐P﹣ABCD,底面是以O為中心的菱形,PO⊥底面ABCD,AB=2,∠BAD= ![]() ,M為BC上的一點,且BM=
,M為BC上的一點,且BM= ![]() ,MP⊥AP.
,MP⊥AP. 
(1)求PO的長;
(2)求二面角A﹣PM﹣C的正弦值.
【答案】
(1)解:連接AC,BD,
∵底面是以O為中心的菱形,PO⊥底面ABCD,
故AC∩BD=O,且AC⊥BD,
以O為坐標原點,OA,OB,OP方向為x,y,z軸正方向建立空間坐標系O﹣xyz,
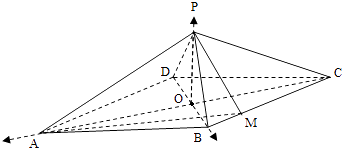
∵AB=2,∠BAD= ![]() ,
,
∴OA=ABcos( ![]() ∠BAD)=
∠BAD)= ![]() ,OB=ABsin(
,OB=ABsin( ![]() ∠BAD)=1,
∠BAD)=1,
∴O(0,0,0),A( ![]() ,0,0),B(0,1,0),C(﹣
,0,0),B(0,1,0),C(﹣ ![]() ,0,0),
,0,0),
![]() =(0,1,0),
=(0,1,0), ![]() =(﹣
=(﹣ ![]() ,﹣1,0),
,﹣1,0),
又∵BM= ![]() ,
,
∴ ![]()
![]() =(﹣
=(﹣ ![]() ,﹣
,﹣ ![]() ,0),
,0),
則 ![]() =
= ![]() +
+ ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,0),
,0),
設P(0,0,a),則 ![]() =(﹣
=(﹣ ![]() ,0,a),
,0,a), ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,a),
,a),
∵MP⊥AP,
∴ ![]()
![]() =
= ![]() ﹣a2=0,
﹣a2=0,
解得a= ![]() ,
,
即PO的長為 ![]() .
.
(2)解:由(1)知 ![]() =(﹣
=(﹣ ![]() ,0,
,0, ![]() ),
), ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,
, ![]() ),
), ![]() =(
=( ![]() ,0,
,0, ![]() ),
),
設平面APM的法向量 ![]() =(x,y,z),平面PMC的法向量為
=(x,y,z),平面PMC的法向量為 ![]() =(a,b,c),
=(a,b,c),
由  ,得
,得 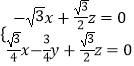 ,
,
令x=1,則 ![]() =(1,
=(1, ![]() ,2),
,2),
由 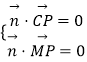 ,得
,得 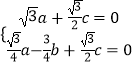 ,
,
令a=1,則 ![]() =(1,﹣
=(1,﹣ ![]() ,﹣2),
,﹣2),
∵平面APM的法向量 ![]() 和平面PMC的法向量
和平面PMC的法向量 ![]() 夾角θ滿足:
夾角θ滿足:
cosθ= ![]() =
= ![]() =﹣
=﹣ ![]()
故sinθ= ![]() =
= ![]()
【解析】(1)連接AC,BD,以O為坐標原點,OA,OB,OP方向為x,y,z軸正方向建立空間坐標系O﹣xyz,分別求出向量 ![]() ,
, ![]() 的坐標,進而根據MP⊥AP,得到
的坐標,進而根據MP⊥AP,得到 ![]()
![]() =0,進而求出PO的長;(2)求出平面APM和平面PMC的法向量,代入向量夾角公式,求出二面角的余弦值,進而根據平方關系可得:二面角A﹣PM﹣C的正弦值
=0,進而求出PO的長;(2)求出平面APM和平面PMC的法向量,代入向量夾角公式,求出二面角的余弦值,進而根據平方關系可得:二面角A﹣PM﹣C的正弦值


科目:高中數學 來源: 題型:
【題目】2015男籃亞錦賽決賽階段,中國男籃以9連勝的不敗戰績贏得第28屆亞錦賽冠軍,同時拿到亞洲唯一1張直通里約奧運會的入場券.賽后,中國男籃主力易建聯榮膺本屆亞錦賽MVP(最有價值球員),下表是易建聯在這9場比賽中投籃的統計數據.
比分 | 易建聯技術統計 | |||
投籃命中 | 罰球命中 | 全場得分 | 真實得分率 | |
中國91﹣42新加坡 | 3/7 | 6/7 | 12 | 59.52% |
中國76﹣73韓國 | 7/13 | 6/8 | 20 | 60.53% |
中國84﹣67約旦 | 12/20 | 2/5 | 26 | 58.56% |
中國75﹣62哈薩克期坦 | 5/7 | 5/5 | 15 | 81.52% |
中國90﹣72黎巴嫩 | 7/11 | 5/5 | 19 | 71.97% |
中國85﹣69卡塔爾 | 4/10 | 4/4 | 13 | 55.27% |
中國104﹣58印度 | 8/12 | 5/5 | 21 | 73.94% |
中國70﹣57伊朗 | 5/10 | 2/4 | 13 | 55.27% |
中國78﹣67菲律賓 | 4/14 | 3/6 | 11 | 33.05% |
注:(1)表中a/b表示出手b次命中a次;
(2)TS%(真實得分率)是衡量球員進攻的效率,其計算公式為:
TS%=.全場得分/2x(投籃出手次數+0.44x罰球出手次數)
(Ⅰ)從上述9場比賽中隨機選擇一場,求易建聯在該場比賽中TS%超過50%的概率;
(Ⅱ)從上述9場比賽中隨機選擇兩場,求易建聯在這兩場比賽中TS%至少有一場超過60%的概率;
(Ⅲ)用x來表示易建聯某場的得分,用y來表示中國隊該場的總分,畫出散點圖如圖所示,請根據散點圖判斷y與x之間是否具有線性相關關系?結合實際簡單說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某旅游景點預計2013年1月份起前x個月的旅游人數的和p(x)(單位:萬人)與x的關系近似地滿足p(x)=![]() x(x+1)(39﹣2x),(x∈N* , 且x≤12).已知第x月的人均消費額q(x)(單位:元)與x的近似關系是q(x)=
x(x+1)(39﹣2x),(x∈N* , 且x≤12).已知第x月的人均消費額q(x)(單位:元)與x的近似關系是q(x)=
(I)寫出2013年第x月的旅游人數f(x)(單位:萬人)與x的函數關系式;
(II)試問2013年第幾月旅游消費總額最大,最大月旅游消費總額為多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示四棱錐![]() 中,
中,![]() 底面
底面![]() ,四邊形
,四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.

![]() 求四棱錐
求四棱錐![]() 的體積;
的體積;
![]() 求證:
求證:![]() 平面
平面![]() ;
;
![]() 在棱
在棱![]() 上是否存在點
上是否存在點![]() 異于點
異于點![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求
,若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高二學生小嚴利用暑假參加社會實踐,為了幫助貿易公司的購物網站優化今年國慶節期間的營銷策略,他對去年10月1日當天在該網站消費且消費金額不超過1000元的1000名(女性800名,男性200名)網購者,根據性別按分層抽樣的方法抽取100名進行分析,得到如下統計圖表(消費金額單位:元):
女性消費情況:
消費金額 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000) |
人數 | 5 | 10 | 15 |
|
|
男性消費情況:
消費金額 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000) |
人數 | 2 | 3 | 10 |
| 2 |
(1)現從抽取的100名且消費金額在[800,1000](單位:元)的網購者中隨機選出兩名發放網購紅包,求選出的這兩名網購者恰好是一男一女的概率;
(2)若消費金額不低于600元的網購者為“網購達人”,低于600元的網購者為“非網購達人”,根據以上統計數據填寫下面![]() 列聯表,并回答能否在犯錯誤的概率不超過0.010的前提下認為“是否為‘網購達人’與性別有關?”
列聯表,并回答能否在犯錯誤的概率不超過0.010的前提下認為“是否為‘網購達人’與性別有關?”
女性 | 男性 | 總計 | |
網購達人 | |||
非網購達人 | |||
總計 |
附:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校藝術節對同一類的![]() ,
,![]() ,
,![]() ,
,![]() 四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“![]() ,
,![]() 兩項作品未獲得一等獎”;
兩項作品未獲得一等獎”;
丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某二手車交易市場對某型號的二手汽車的使用年數![]() 與銷售價格
與銷售價格![]() (單位:萬元/輛)進行整理,得到如下的對應數據:
(單位:萬元/輛)進行整理,得到如下的對應數據:
使用年數 | 2 | 4 | 6 | 8 | 10 |
售價 | 16 | 13 | 9.5 | 7 | 4.5 |
(1)試求![]() 關于
關于![]() 的回歸直線方程:(參考公式:
的回歸直線方程:(參考公式: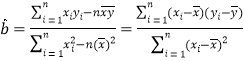 ,
, ![]() .)
.)
(2)已知每輛該型號汽車的收購價格為![]() 萬元,根據(1)中所求的回歸方程,預測
萬元,根據(1)中所求的回歸方程,預測![]() 為何值時,銷售一輛該型號汽車所獲得的利潤
為何值時,銷售一輛該型號汽車所獲得的利潤![]() 最大?
最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋中混裝著9個大小相同的球(編號不同),其中5只白球,4只紅球,為了把紅球與白球區分開來,采取逐只抽取檢查,若恰好經過5次抽取檢查,正好把所有白球和紅球區分出來了,則這樣的抽取方式共有__________種(用數字作答) .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com