
【題目】從某校高三上學期期末數學考試成績中,隨機抽取了![]() 名學生的成績得到頻率分布直方圖如下:
名學生的成績得到頻率分布直方圖如下:
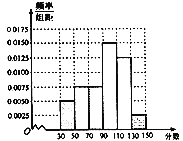
(1)若用分層抽樣的方法從分數在![]() 和
和![]() 的學生中共抽取
的學生中共抽取![]() 人,該
人,該![]() 人中成績在
人中成績在![]() 的有幾人?
的有幾人?
(2)在(1)中抽取的![]() 人中,隨機抽取
人中,隨機抽取![]() 人,求分數在
人,求分數在![]() 和
和![]() 各
各![]() 人的概率.
人的概率.
(3)根據頻率分布直方圖,估計該校高三學生本次數學考試的平均分;
【答案】(1)1(2)![]() (3)92
(3)92
【解析】試題分析:
(1)結合抽樣比可得該![]() 人中成績在
人中成績在![]() 的有1人;
的有1人;
(2)利用題意寫出所有可能的情形,結合古典概型公式可得概率![]() ;
;
(3)結合頻率分布直方圖可估計該校高三學生本次數學考試的平均分為92分.
試題解析:
(1)樣本中分數在[30,50)和[130,150]的人數分別為6人和3人
所以抽取的3人中分數在[130,150]的人有![]() (人)
(人)
(2)由(1)知:抽取的3人中分數在[30,50)的有2人,記為![]() ;分數在[130,150]的人有1人,記為
;分數在[130,150]的人有1人,記為![]() ,從中隨機抽取2人,總的情形有
,從中隨機抽取2人,總的情形有![]() 三種.
三種.
而分數在[30,50)和[130,150]各1人的情形有![]() 兩種,故所求概率
兩種,故所求概率![]()
(3)由頻率分布直方圖,得該校高三學生本次數學考試的平均分為
0.0050×20×40+0.0075×20×60+0.0075×20×80+0.0150×20×100+0.0125×20×120+0.0025×20×140=92.


科目:高中數學 來源: 題型:
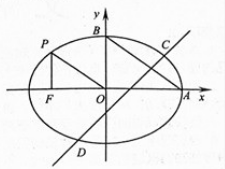
【題目】如圖,過橢圓![]() 上一點
上一點![]() 向
向![]() 軸作垂線,垂足為左焦點
軸作垂線,垂足為左焦點![]() ,
,![]() 分別為
分別為![]() 的右頂點,上頂點,且
的右頂點,上頂點,且![]() ,
,![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)![]() 為
為![]() 上的兩點,若四邊形
上的兩點,若四邊形![]()
![]() 逆時針排列)的對角線
逆時針排列)的對角線![]() 所在直線的斜率為
所在直線的斜率為![]() ,求四邊形
,求四邊形![]() 面積
面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
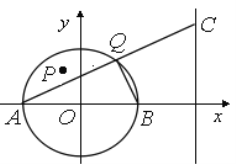
【題目】已知圓![]() ,直線
,直線![]() :x=6,圓
:x=6,圓![]() 與
與![]() 軸相交于點
軸相交于點![]() (如圖),點P(-1,2)是圓
(如圖),點P(-1,2)是圓![]() 內一點,點
內一點,點![]() 為圓
為圓![]() 上任一點(異于點
上任一點(異于點![]() ),直線
),直線![]() 與
與![]() 相交于點
相交于點![]() .
.
(1)若過點P的直線![]() 與圓
與圓![]() 相交所得弦長等于
相交所得弦長等于![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)設直線![]() 的斜率分別為
的斜率分別為![]() ,求證:
,求證: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠家計劃在2012年舉行商品促銷活動,經調查測算,該商品的年銷售量![]() 萬件與年促銷費用
萬件與年促銷費用![]() 萬元滿足:
萬元滿足:![]() ,其中
,其中![]() 為常數,若不搞促銷活動,則該產品的年銷售量只有1萬件,已知2012年生產該產品的固定投入為8萬元,每生產1萬件該產品需要再投入16萬元,廠家的產量等于銷售量,而銷售收入為生產成本的1.5倍(生產成本由固定投入和再投入兩部分資金組成).
為常數,若不搞促銷活動,則該產品的年銷售量只有1萬件,已知2012年生產該產品的固定投入為8萬元,每生產1萬件該產品需要再投入16萬元,廠家的產量等于銷售量,而銷售收入為生產成本的1.5倍(生產成本由固定投入和再投入兩部分資金組成).
(1)將2012年該產品的利潤![]() 萬元表示為年促銷費用
萬元表示為年促銷費用![]() 萬元的函數;
萬元的函數;
(2)該廠2012年的促銷費用投入多少萬元時,廠家的利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】未知數的個數多余方程個數的方程(組)叫做不定方程,最早提出不定方程的是我國的《九章算術》.實際生活中有很多不定方程的例子,例如“百雞問題”:公元五世紀末,我國古代數學家張丘建在《算經》中提出了“百雞問題”:“雞母一,值錢三;雞翁一,值錢二;雞雛二,值錢一.百錢買百雞,問雞翁、母、雛各幾何?”
算法設計:
(1)設母雞、公雞、小雞數分別為![]() 、
、![]() 、
、![]() ,則應滿足如下條件:
,則應滿足如下條件:
![]() ;
;![]() .
.
(2)先分析一下三個變量的可能值.①![]() 的最小值可能為零,若全部錢用來買母雞,最多只能買33只,
的最小值可能為零,若全部錢用來買母雞,最多只能買33只,
故![]() 的值為
的值為![]() 中的整數.②
中的整數.②![]() 的最小值為零,最大值為50.③
的最小值為零,最大值為50.③![]() 的最小值為零,最大值為100.
的最小值為零,最大值為100.
(3)對![]() 、
、![]() 、
、![]() 三個未知數來說,
三個未知數來說,![]() 取值范圍最少.為提高程序的效率,先考慮對
取值范圍最少.為提高程序的效率,先考慮對![]() 的值進行一一列舉.
的值進行一一列舉.
(4)在固定一個![]() 的值的前提下,再對
的值的前提下,再對![]() 值進行一一列舉.
值進行一一列舉.
(5)對于每個![]() ,
,![]() ,怎樣去尋找滿足百年買百雞條件的
,怎樣去尋找滿足百年買百雞條件的![]() .由于
.由于![]() ,
,![]() 值已設定,便可由下式得到:
值已設定,便可由下式得到:![]() .
.
(6)這時的![]() ,
,![]() ,
,![]() 是一組可能解,它只滿足“百雞”條件,還未滿足“百錢”.是否真實解,還要看它們是否滿足
是一組可能解,它只滿足“百雞”條件,還未滿足“百錢”.是否真實解,還要看它們是否滿足![]() ,滿足即為所求解.
,滿足即為所求解.
根據上述算法思想,畫出流程圖并用偽代碼表示.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某地參加2015 年夏令營的![]() 名學生的身體健康情況,將學生編號為
名學生的身體健康情況,將學生編號為![]() ,采用系統抽樣的方法抽取一個容量為
,采用系統抽樣的方法抽取一個容量為![]() 的樣本,且抽到的最小號碼為
的樣本,且抽到的最小號碼為![]() ,已知這
,已知這![]() 名學生分住在三個營區,從
名學生分住在三個營區,從![]() 到
到![]() 在第一營區,從
在第一營區,從![]() 到
到![]() 在第二營區,從
在第二營區,從![]() 到
到![]() 在第三營區,則第一、第二、第三營區被抽中的人數分別為( )
在第三營區,則第一、第二、第三營區被抽中的人數分別為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() ,
,![]() ,其前
,其前![]() 項和
項和![]() 滿足
滿足![]() ,其中
,其中![]() .
.
(1)設![]() ,證明:數列
,證明:數列![]() 是等差數列;
是等差數列;
(2)設![]() ,
,![]() 為數列
為數列![]() 的前
的前![]() 項和,求證:
項和,求證:![]() ;
;
(3)設![]() (
(![]() 為非零整數,
為非零整數,![]() ),試確定
),試確定![]() 的值,使得對任意
的值,使得對任意![]() ,都有
,都有![]() 成立.
成立.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com