Question

【題目】設(shè)函數(shù)，，(其中).

（1）時,求函數(shù)的極值;

（2）證：存在，使得在內(nèi)恒成立，且方程在內(nèi)有唯一解.

Answer 1

【答案】(1) ；;(2)見解析.

【解析】

（Ⅰ）求出函數(shù)的導(dǎo)數(shù)，解關(guān)于導(dǎo)函數(shù)的不等式，求出函數(shù)的單調(diào)區(qū)間，從而求出函數(shù)的極值即可；

（Ⅱ）求出f（x）的導(dǎo)數(shù)，通過討論m的范圍，求出f（x）的單調(diào)區(qū)間，求出滿足條件的m的范圍，從而證出結(jié)論即可．

解：（I）當(dāng)時, ,

令,得,,當(dāng)變化時,的變化如下表:

		極大值		極小值

由表可知,；；

（II）設(shè)，，，若要有解，需有單減區(qū)間，則要有解

，由，，記為函數(shù)的導(dǎo)數(shù)

則 ，當(dāng)時單增，令，由，得，需考察與區(qū)間的關(guān)系：

①當(dāng)時，，，在上，單增，

故單增，，無解；

②當(dāng)，時，，，因為單增，在上，在上

當(dāng)時，

（i）若，即時，，單增，，無解；

（ii）若，即，，在上，，單減；，，在區(qū)間上有唯一解，記為；在上，單增 ，，當(dāng)時，故在區(qū)間上有唯一解，記為，則在上，在上，在上，當(dāng)時，取得最小值，此時

若要恒成立且有唯一解，當(dāng)且僅當(dāng)，即，由有

聯(lián)立兩式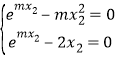解得.綜上，當(dāng)時，