
已知三棱錐S-ABC的所有頂點(diǎn)都在球O的球面上,SA⊥平面ABC,SA=2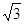 ,AB=1,AC=2,∠BAC=60°,則球O的表面積為
,AB=1,AC=2,∠BAC=60°,則球O的表面積為
A.4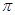 | B.12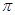 | C.16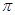 | D.64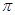 |
C
解析試題分析:由三棱錐S-ABC的所有頂點(diǎn)都在球O的球面上,SA⊥平面ABC,SA="2" 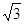 ,AB=1,AC=2,∠BAC=60°,知BC=
,AB=1,AC=2,∠BAC=60°,知BC=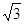 ,∠ABC=90°.故△ABC截球O所得的圓O′的半徑r=
,∠ABC=90°.故△ABC截球O所得的圓O′的半徑r= AC=1,由此能求出球O的半徑,從而能求出球O的表面積。解:如圖,
AC=1,由此能求出球O的半徑,從而能求出球O的表面積。解:如圖,
三棱錐S-ABC的所有頂點(diǎn)都在球O的球面上,∵SA⊥平面ABC,SA=2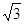 ,AB=1,AC=2,∠BAC=60°,∴BC=
,AB=1,AC=2,∠BAC=60°,∴BC=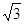 ,∴∠ABC=90°.∴△ABC截球O所得的圓O′的半徑r=
,∴∠ABC=90°.∴△ABC截球O所得的圓O′的半徑r= AC=1,∴球O的半徑R=
AC=1,∴球O的半徑R=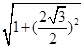 =2,∴球O的表面積S=4πR2=16π.故選C.
=2,∴球O的表面積S=4πR2=16π.故選C.
考點(diǎn):球的表面積
點(diǎn)評(píng):本題考查球的表面積的求法,合理地作出圖形,數(shù)形結(jié)合求出球半徑,是解題時(shí)要關(guān)鍵.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:單選題
點(diǎn)A、B、C、D在同一個(gè)球的球面上,AB=BC= , AC=2,若四面體ABCD體積的最大值為
, AC=2,若四面體ABCD體積的最大值為 ,則這個(gè)球的表面積為
,則這個(gè)球的表面積為
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
如圖, 正三棱柱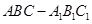 的主視圖(又稱正視圖)是邊長為4的正方形, 則此正三棱柱的側(cè)視圖(又稱左視圖)的面積為( )
的主視圖(又稱正視圖)是邊長為4的正方形, 則此正三棱柱的側(cè)視圖(又稱左視圖)的面積為( )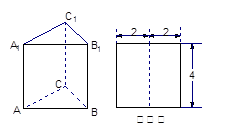
A.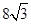 | B. | C. | D.16 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com