
【題目】設拋物線C:y2=2px(p>0)的焦點為F,點M在C上,|MF|=5,若以MF為直徑的圓過點(0,2),則C的方程為( )
A.y2=4x或y2=8x
B.y2=2x或y2=8x
C.y2=4x或y2=16x
D.y2=2x或y2=16x
【答案】C
【解析】解:∵拋物線C方程為y2=2px(p>0),
∴焦點F坐標為( ![]() ,0),可得|OF|=
,0),可得|OF|= ![]() ,
,
∵以MF為直徑的圓過點(0,2),
∴設A(0,2),可得AF⊥AM,
Rt△AOF中,|AF|= ![]() =
= ![]() ,
,
∴sin∠OAF= ![]() =
= ![]() ,
,
∵根據(jù)拋物線的定義,得直線AO切以MF為直徑的圓于A點,
∴∠OAF=∠AMF,可得Rt△AMF中,sin∠AMF= ![]() =
= ![]() ,
,
∵|MF|=5,|AF|= ![]()
∴ ![]() =
= ![]() ,整理得4+
,整理得4+ ![]() =
= ![]() ,解之可得p=2或p=8
,解之可得p=2或p=8
因此,拋物線C的方程為y2=4x或y2=16x.
故選:C.
方法二:
∵拋物線C方程為y2=2px(p>0),∴焦點F( ![]() ,0),
,0),
設M(x,y),由拋物線性質(zhì)|MF|=x+ ![]() =5,可得x=5﹣
=5,可得x=5﹣ ![]() ,
,
因為圓心是MF的中點,所以根據(jù)中點坐標公式可得,圓心橫坐標為 ![]() =
= ![]() ,
,
由已知圓半徑也為 ![]() ,據(jù)此可知該圓與y軸相切于點(0,2),故圓心縱坐標為2,則M點縱坐標為4,
,據(jù)此可知該圓與y軸相切于點(0,2),故圓心縱坐標為2,則M點縱坐標為4,
即M(5﹣ ![]() ,4),代入拋物線方程得p2﹣10p+16=0,所以p=2或p=8.
,4),代入拋物線方程得p2﹣10p+16=0,所以p=2或p=8.
所以拋物線C的方程為y2=4x或y2=16x.
故答案C.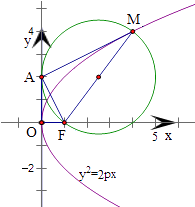


 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】某中學為研究學生的身體素質(zhì)與課外體育鍛煉時間的關系,對該校200名高三學生平均每天課外體育鍛煉時間進行調(diào)查,如表:(平均每天鍛煉的時間單位:分鐘)
平均每天鍛煉的時間/分鐘 |
|
|
|
|
|
|
總人數(shù) | 20 | 36 | 44 | 50 | 40 | 10 |
將學生日均課外體育鍛煉時間在![]() 的學生評價為“課外體育達標”.
的學生評價為“課外體育達標”.
(1)請根據(jù)上述表格中的統(tǒng)計數(shù)據(jù)填寫下面的![]() 列聯(lián)表;
列聯(lián)表;
課外體育不達標 | 課外體育達標 | 合計 | |
男 | |||
女 | 20 | 110 | |
合計 |
(2)通過計算判斷是否能在犯錯誤的概率不超過![]() 的前提下認為“課外體育達標”性別有關?
的前提下認為“課外體育達標”性別有關?
參考公式![]() ,其中
,其中![]()
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】通過隨機詢問110名不同的大學生是否愛好某項運動,得到如下的列聯(lián)表:
經(jīng)計算![]() 的觀測值
的觀測值![]() . 參照附表,得到的正確結論是
. 參照附表,得到的正確結論是
附表:
男 | 女 | 總計 | |
愛好 | 40 | 20 | 60 |
不愛好 | 20 | 30 | 50 |
總計 | 60 | 50 | 110 |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
A. 有99%以上的把握認為“愛好該項運動與性別有關”
B. 有99%以上的把握認為“愛好該項運動與性別無關”
C. 在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別有關”
D. 在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別無關”
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)= ![]() ,a為常數(shù)且a>0.
,a為常數(shù)且a>0.
(1)f(x)的圖象關于直線x= ![]() 對稱;
對稱;
(2)若x0滿足f(f(x0))=x0 , 但f(x0)≠x0 , 則x0稱為函數(shù)f(x)的二階周期點,如果f(x)有兩個二階周期點x1 , x2 , 試確定a的取值范圍;
(3)對于(2)中的x1 , x2 , 和a,設x3為函數(shù)f(f(x))的最大值點,A(x1 , f(f(x1))),B(x2 , f(f(x2))),C(x3 , 0),記△ABC的面積為S(a),討論S(a)的單調(diào)性.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某校從高二年級學生中隨機抽取60名學生,將期中考試的政治成績(均為整數(shù))分成六段:![]() 后得到如下頻率分布直方圖.
后得到如下頻率分布直方圖.
(1)根據(jù)頻率分布直方圖,分別求![]() ,眾數(shù),中位數(shù)。
,眾數(shù),中位數(shù)。
(2)估計該校高二年級學生期中考試政治成績的平均分。
(3)用分層抽樣的方法在各分數(shù)段的學生中抽取一個容量為20的樣本,則在![]() 分數(shù)段抽取的人數(shù)是多少?
分數(shù)段抽取的人數(shù)是多少?
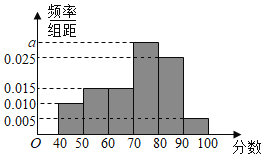
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知點A是以BC為直徑的圓O上異于B,C的動點,P為平面ABC外一點,且平面PBC⊥平面ABC,BC=3,PB=2![]() ,PC
,PC![]() ,則三棱錐P﹣ABC外接球的表面積為______.
,則三棱錐P﹣ABC外接球的表面積為______.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】對于棱長為![]() 的正方體
的正方體![]() ,有如下結論,其中錯誤的是( )
,有如下結論,其中錯誤的是( )
A. 以正方體的頂點為頂點的幾何體可以是每個面都為直角三角形的四面體;
B. 過點![]() 作平面
作平面![]() 的垂線,垂足為點
的垂線,垂足為點![]() ,則
,則![]() 三點共線;
三點共線;
C. 過正方體中心的截面圖形不可能是正六邊形;
D. 三棱錐![]() 與正方體的體積之比為
與正方體的體積之比為![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知雙曲線C: ![]() =1(a>0,b>0)的左、右焦點分別為F1 , F2 , 離心率為3,直線y=2與C的兩個交點間的距離為
=1(a>0,b>0)的左、右焦點分別為F1 , F2 , 離心率為3,直線y=2與C的兩個交點間的距離為 ![]() .
.
(1)求a,b;
(2)設過F2的直線l與C的左、右兩支分別相交于A、B兩點,且|AF1|=|BF1|,證明:|AF2|、|AB|、|BF2|成等比數(shù)列.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com