
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的極值;
的極值;
(2)若不等式![]() 恒成立,求
恒成立,求![]() 的最小值(其中e為自然對數(shù)的底數(shù)).
的最小值(其中e為自然對數(shù)的底數(shù)).
【答案】(1)當![]() 時,
時,![]() 無極值;當
無極值;當![]() 時,
時,![]() 極大值為
極大值為![]() ,無極小值
,無極小值
(2)-1
【解析】
(1)求出導函數(shù)![]() ,確定函數(shù)單調(diào)性,得極值,需分類討論.
,確定函數(shù)單調(diào)性,得極值,需分類討論.
(2)![]() 恒成立,設(shè)
恒成立,設(shè)![]() ,求出
,求出![]() 的最大值
的最大值![]() ,由
,由![]() 得出
得出![]() 滿足的不等關(guān)系
滿足的不等關(guān)系![]() ,然后得
,然后得![]() ,求得
,求得![]() 的最小值即得結(jié)論.
的最小值即得結(jié)論.
(1)解![]() ,
,
當![]() 時,
時,![]() 恒成立,函數(shù)
恒成立,函數(shù)![]() 在
在![]() 上單調(diào)遞增,無極值.
上單調(diào)遞增,無極值.
當![]() 時,由
時,由![]() ,得
,得![]() ,函數(shù)
,函數(shù)![]() 在
在![]() 上單調(diào)遞增,由
上單調(diào)遞增,由![]() ,得
,得![]() ,
,
函數(shù)![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,![]() 極大值為
極大值為![]() ,無極小值.
,無極小值.
綜上所述,當![]() 時,
時,![]() 無極值;
無極值;
當![]() 時,
時,![]() 極大值為
極大值為![]() ,無極小值.
,無極小值.
(2)由![]() 可得
可得![]() ,
,
設(shè)![]() ,所以
,所以![]() ,
,![]() ,
,
當![]() 時,
時,![]() ,
,![]() 在
在![]() 上是增函數(shù),所以
上是增函數(shù),所以![]() 不可能恒成立,
不可能恒成立,
當![]() 時,由
時,由![]() ,得
,得![]() ,
,
當![]() 時,
時,![]() ,
,![]() 單調(diào)遞增,當
單調(diào)遞增,當![]() 時,
時,![]() ,
,![]() 單調(diào)遞減,
單調(diào)遞減,
所以當![]() 時,
時,![]() 取最大值,
取最大值,![]() ,
,
所以![]() ,即
,即![]() ,所以
,所以![]() ,
,
令![]() ,
,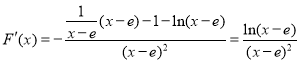 ,
,
當![]() 時,
時,![]() ,
,![]() 單調(diào)遞增,
單調(diào)遞增,
當![]() 時,
時,![]() ,
,![]() 單調(diào)遞減,
單調(diào)遞減,
所以當![]() 時,
時,![]() 取最小值,即
取最小值,即![]() ,所以
,所以![]() 的最小值為-1.
的最小值為-1.


 智慧小復習系列答案
智慧小復習系列答案科目:高中數(shù)學 來源: 題型:
【題目】勞動教育是中國特色社會主義教育制度的重要內(nèi)容,某高中計劃組織學生參與各項職業(yè)體驗,讓學生在勞動課程中掌握一定勞動技能,理解勞動創(chuàng)造價值,培養(yǎng)勞動自立意識和主動服務他人、服務社會的情懷.學校計劃下周在高一年級開設(shè)“縫紉體驗課”,聘請“織補匠人”李阿姨給同學們傳授織補技藝。高一年級有6個班,李阿姨每周一到周五只有下午第2節(jié)課的時間可以給同學們上課,所以必須安排有兩個班合班上課,高一年級6個班“縫紉體驗課”的不同上課順序有( )
A.600種B.3600種C.1200種D.1800種
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,在平行四邊形ABCD中,![]() ,
,![]() ,
,![]() ,點E是CD邊的中點,將
,點E是CD邊的中點,將![]() 沿AE折起,使點D到達點P的位置,且
沿AE折起,使點D到達點P的位置,且![]() .
.

(1)求證;平面![]() 平面ABCE;
平面ABCE;
(2)求點E到平面PAB的距離.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】手機等數(shù)碼產(chǎn)品中的存儲器核心部件是閃存芯片,閃存芯片有兩個獨立的性能指標:數(shù)據(jù)傳輸速度和使用壽命,數(shù)據(jù)傳輸速度的單位是![]() ,使用壽命指的是完全擦寫的次數(shù)(單位:萬次).某閃存芯片制造廠為了解產(chǎn)品情況,從一批閃存芯片中隨機抽取了100件作為樣本進行性能測試,測試數(shù)據(jù)經(jīng)過整理得到如下的頻率分布直方圖(每個分組區(qū)間均為左閉右開),其中
,使用壽命指的是完全擦寫的次數(shù)(單位:萬次).某閃存芯片制造廠為了解產(chǎn)品情況,從一批閃存芯片中隨機抽取了100件作為樣本進行性能測試,測試數(shù)據(jù)經(jīng)過整理得到如下的頻率分布直方圖(每個分組區(qū)間均為左閉右開),其中![]() ,
,![]() ,
,![]() 成等差數(shù)列且
成等差數(shù)列且![]() .
.


(1)估計樣本中閃存芯片的數(shù)據(jù)傳輸速度的中位數(shù).
(2)估計樣本中閃存芯片的使用壽命的平均數(shù).(每組數(shù)據(jù)以中間值為代表)
(3)規(guī)定數(shù)據(jù)傳輸速度不低于![]() 為優(yōu),使用壽命不低于10萬次為優(yōu),且兩項指標均為優(yōu)的閃存芯片為
為優(yōu),使用壽命不低于10萬次為優(yōu),且兩項指標均為優(yōu)的閃存芯片為![]() 級產(chǎn)品,僅有一項為優(yōu)的為
級產(chǎn)品,僅有一項為優(yōu)的為![]() 級產(chǎn)品,沒有優(yōu)的為
級產(chǎn)品,沒有優(yōu)的為![]() 級產(chǎn)品.現(xiàn)已知樣本中有45件
級產(chǎn)品.現(xiàn)已知樣本中有45件![]() 級產(chǎn)品,用樣本中不同級別產(chǎn)品的頻率代替每件產(chǎn)品為相應級別的概率,從這一批產(chǎn)品中任意抽取4件,求其中至少有2件
級產(chǎn)品,用樣本中不同級別產(chǎn)品的頻率代替每件產(chǎn)品為相應級別的概率,從這一批產(chǎn)品中任意抽取4件,求其中至少有2件![]() 級產(chǎn)品的概率.
級產(chǎn)品的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖:已知四棱錐P—ABCD的底面ABCD是平行四邊形,PA⊥面ABCD,M是AD的中點,N是PC的中點.

(1)求證:MN∥面PAB;
(2)若平面PMC⊥面PAD,求證:CM⊥AD.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為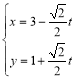 (
(![]() 為參數(shù)),在以坐標原點為極點,
為參數(shù)),在以坐標原點為極點,![]() 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線![]() 的方程為
的方程為![]() .
.
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設(shè)曲線![]() 與直線
與直線![]() 交于點
交于點![]() ,點
,點![]() 的坐標為(3,1),求
的坐標為(3,1),求![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
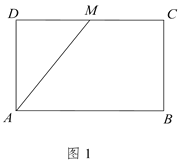
【題目】如圖1所示,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 中點,將
中點,將![]() 沿
沿![]() 折起,使點
折起,使點![]() 到點
到點![]() 處,且平面
處,且平面![]() 平面
平面![]() ,如圖2所示.
,如圖2所示.
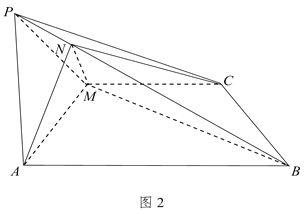
(1)求證:![]() :
:
(2)在棱![]() 上取點
上取點![]() ,使平面
,使平面![]() 平面
平面![]() ,求平面
,求平面![]() 與
與![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
已知曲線![]() 在平面直角坐標系
在平面直角坐標系![]() 下的參數(shù)方程為
下的參數(shù)方程為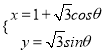 (
(![]() 為參數(shù)),以坐標原點
為參數(shù)),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系.
軸正半軸為極軸,建立極坐標系.
(1)求曲線![]() 的普通方程及極坐標方程;
的普通方程及極坐標方程;
(2)直線![]() 的極坐標方程是
的極坐標方程是![]() ,射線
,射線![]() :
: ![]() 與曲線
與曲線![]() 交于點
交于點![]() 與直線
與直線![]() 交于點
交于點![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com