
【題目】如圖,在三棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點.
的中點.
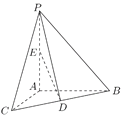
(1)求三棱錐![]() 的體積;
的體積;
(2)若異面直線![]() 與
與![]() 所成的角為
所成的角為![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)三棱錐P﹣ABC中,由PA⊥平面ABC,AC⊥AB,利用VP﹣ABC![]() PA能求出三棱錐P﹣ABC的體積.
PA能求出三棱錐P﹣ABC的體積.
(2)取AC中點F,連接DF,EF,則AB∥DF,得∠EDF(或其補角)就是異面直線AB與ED所成的角θ,由此能求出tanθ.
(1)三棱錐P﹣ABC中,
∵PA⊥平面ABC,AC⊥AB,AP=BC=4,∠ABC=30°,D、E分別是BC、AP的中點,
∴AC=2,AB=2![]() ,
,
所以,體積VP﹣ABC![]() PA
PA![]() .
.
(2)取AC中點F,連接DF,EF,則AB∥DF,
所以∠EDF(或其補角)就是異面直線AB與ED所成的角θ.
由已知,AC=EA=AD=2,AB=2![]() ,PC=2
,PC=2![]() ,
,
∵AB⊥EF,∴DF⊥EF.
在Rt△EFD中,DF![]() ,EF
,EF![]() ,
,
所以,tanθ![]() .
.



 王后雄學(xué)案教材完全解讀系列答案
王后雄學(xué)案教材完全解讀系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)為了檢查生產(chǎn)![]() 產(chǎn)品的甲、乙兩條流水線的生產(chǎn)情況,隨機地從這兩條流水線上生產(chǎn)的大量產(chǎn)品中各抽取50件產(chǎn)品作為樣本,測出它們的這一項質(zhì)量指標(biāo)值.若該項質(zhì)量指標(biāo)值落在
產(chǎn)品的甲、乙兩條流水線的生產(chǎn)情況,隨機地從這兩條流水線上生產(chǎn)的大量產(chǎn)品中各抽取50件產(chǎn)品作為樣本,測出它們的這一項質(zhì)量指標(biāo)值.若該項質(zhì)量指標(biāo)值落在![]() 內(nèi),則為合格品,否則為不合格品.下表是甲流水線樣本的頻數(shù)分布表,下圖是乙流水線樣本的頻率分布直方圖.
內(nèi),則為合格品,否則為不合格品.下表是甲流水線樣本的頻數(shù)分布表,下圖是乙流水線樣本的頻率分布直方圖.
甲流水線樣本的頻數(shù)分布表
質(zhì)量指標(biāo)值 | 頻數(shù) |
| 9 |
| 10 |
| 17 |
| 8 |
| 6 |
乙流水線樣本的頻率分布直方圖
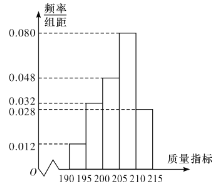
(1)根據(jù)圖形,估計乙流水線生產(chǎn)的![]() 產(chǎn)品的該項質(zhì)量指標(biāo)值的中位數(shù);
產(chǎn)品的該項質(zhì)量指標(biāo)值的中位數(shù);
(2)設(shè)該企業(yè)生產(chǎn)一件合格品獲利100元,生產(chǎn)一件不合格品虧損50元,若某個月內(nèi)甲、乙兩條流水線均生產(chǎn)了1000件產(chǎn)品,若將頻率視為概率,則該企業(yè)本月的利潤約為多少元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 與橢圓
與橢圓![]() 有一個相同的焦點,過點
有一個相同的焦點,過點![]() 且與
且與![]() 軸不垂直的直線
軸不垂直的直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() 兩點,
兩點,![]() 關(guān)于
關(guān)于![]() 軸的對稱點為
軸的對稱點為![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)試問直線![]() 是否過定點?若是,求出該定點的坐標(biāo);若不是,請說明理由.
是否過定點?若是,求出該定點的坐標(biāo);若不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖正方體![]() 的棱長為a,以下結(jié)論不正確的是( )
的棱長為a,以下結(jié)論不正確的是( )

A. 異面直線![]() 與
與![]() 所成的角為
所成的角為![]()
B. 直線![]() 與
與![]() 垂直
垂直
C. 直線![]() 與
與![]() 平行
平行
D. 三棱錐![]() 的體積為
的體積為![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩人玩猜數(shù)字游戲,先由甲心中任想一個數(shù)字,記為![]() ,再由乙猜甲剛才想的數(shù)字把乙猜的數(shù)字記為
,再由乙猜甲剛才想的數(shù)字把乙猜的數(shù)字記為![]() ,且
,且![]() ,若
,若![]() ,則稱甲乙“心有靈犀”,現(xiàn)任意找兩個人玩這個游戲,得出他們“心有靈犀”的概率為________
,則稱甲乙“心有靈犀”,現(xiàn)任意找兩個人玩這個游戲,得出他們“心有靈犀”的概率為________
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是邊
是邊![]() 上一點,且
上一點,且![]() ,點
,點![]() 是
是![]() 的中點,將
的中點,將![]() 沿著
沿著![]() 折起,使點
折起,使點![]() 運動到點
運動到點![]() 處,且滿足
處,且滿足![]() .
.
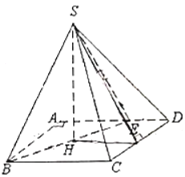
(1)證明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)函數(shù)![]() 是否有極值?若有,求出極值;若沒有,說明理由.
是否有極值?若有,求出極值;若沒有,說明理由.
(2)若對任意![]() ,
,![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com