【題目】設整數
模2014互不同余，整數
模2014也互不同余.證明：可將重新排列為
，使得
模4028互不同余.
【答案】見解析
【解析】
記
.不妨設
.
對每個整數
，若
，
則令
；
否則，令
.
若為前一種情形， 則
.
若為后一種情形，則
.
若不然，有
，
.
上面兩式相加得
.
于是，
.
但
模2014（=2k）互不同余，特別地，
，矛盾.
由上述構造方法知
模4k互不同余.即只需證明結論：對任意整數
，
模4k兩兩不同余.
注意到，前面的構造方式已保證
. ①
[情形1]
，且
.
則由前面的構造方式知
，
.
由于
，故易知
與
及
模2k不同余，
與及
模2k不同余，從而，模4k更不同余，再結合式①，結論得證.
[情形2]
，且
.
則由前面的構造方式知
，
.
同樣有與及模2k不同余，與及模2k不同余.
與情形1相同知結論得證.
[情形3] ，且（，且的情形與此相同）.
則由前面的構造方式知
，
.
由于k為奇數，則
.
故
.
因此，與及模2k不同余，與及模2k不同余.從而，結論得證.
綜上，本題得證.
活力課時同步練習冊系列答案科目：高中數學 來源： 題型：
【題目】如圖，
是半圓
的直徑，
，
為圓周上一點，
平面
，
，
，
，
.
（1）求證：平面
平面
；
（2）在線段
上是否存在點
，且使得
平面？若存在，求出點的位置；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
為偶函數.
（1）求實數
的值；
（2）若不等式
恒成立，求實數a的取值范圍；
（3）若函數
，
，是否存在實數m，使得
的最小值為2，若存在，請求出m的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某媒體為調查喜愛娛樂節目A是否與觀眾性別有關，隨機抽取了30名男性和30名女性觀眾，抽查結果用等高條形圖表示如圖：
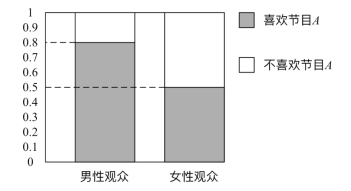
根據該等高條形圖，完成下列2×2列聯表，并用獨立性檢驗的方法分析，能否在犯錯誤的概率不超過0.05的前提下認為喜歡娛樂節目A與觀眾性別有關？
喜歡節目A | 不喜歡節目A | 總計 | |
男性觀眾 | |||
女性觀眾 | |||
總計 | 60 |
附：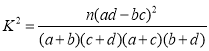
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某二手車直賣網站對其所經營的一款品牌汽車的使用年數x與銷售價格y(單位：萬元，輛)進行了記錄整理，得到如下數據：
(I)畫散點圖可以看出，z與x有很強的線性相關關系，請求出z與x的線性回歸方程(回歸系數
精確到0.01)；
(II)求y關于x的回歸方程，并預測某輛該款汽車當使用年數為10年時售價約為多少．
參考公式：
參考數據：
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知集合M＝{x|x<－3，或x>5}，P＝{x|(x－a)·(x－8)≤0}．
(1)求M∩P＝{x|5<x≤8}的充要條件；
(2)求實數a的一個值，使它成為M∩P＝{x|5<x≤8}的一個充分但不必要條件．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
