
【題目】已知定義域為![]() 的單調遞減的奇函數
的單調遞減的奇函數![]() ,當
,當![]() 時,
時, ![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)若對任意的![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)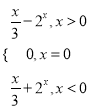 ;(3)
;(3)![]() .
.
【解析】試題分析:(1)根據函數為奇函數得![]() ,結合當
,結合當![]() 時,
時, ![]() ,即可求出
,即可求出![]() 的值;(2)由定義域為
的值;(2)由定義域為![]() 的函數
的函數![]() 是奇函數,知
是奇函數,知![]() .當
.當![]() 時,
時, ![]() ,由函數
,由函數![]() 是奇函數,知
是奇函數,知![]() ,由此能求出
,由此能求出![]() 的解析式;(3)由
的解析式;(3)由![]() 是
是![]() 上單調遞減的奇函數,
上單調遞減的奇函數, ![]() ,得
,得![]() 即
即![]() 恒成立,再由根的判別式小于零即可求出實數
恒成立,再由根的判別式小于零即可求出實數![]() 的取值范圍.
的取值范圍.
試題解析:(1)f(﹣1)=﹣f(1)=﹣(![]() ﹣2)=
﹣2)=![]() ;
;
(2)∵定義域為R的函數f(x)是奇函數,
∴f(0)=0,
當x<0時,﹣x>0,
f(﹣x)=﹣![]() ﹣2﹣x ,
﹣2﹣x ,
又∵函數f(x)是奇函數,
∴f(﹣x)=﹣f(x),
∴f(x)=![]() +2﹣x ,
+2﹣x ,
綜上所述f(x)=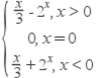 .
.
(3)∵f(1)=﹣![]() <f(0)=0,
<f(0)=0,
且f(x)在R上單調,
∴f(x)在R上單調遞減,
由f(t2﹣2t)+f(2t2﹣k)<0,
得f(t2﹣2t)<﹣f(2t2﹣k),
∵f(x)是奇函數,
∴f(t2﹣2t)<f(k﹣2t2),
又∵f(x)是減函數,
∴t2﹣2t>k﹣2t2
即3t2﹣2t﹣k>0對任意t∈R恒成立,
∴△=4+12k<0得k<﹣![]() ,即為所求.
,即為所求.


科目:高中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,已知AB=a,BC=b(a>b),在AB,AD,CB,CD上,分別截取AE=AH=CF=CG=x(x>0),設四邊形EFGH的面積為y.
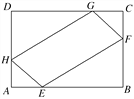
(1)寫出四邊形EFGH的面積y與x之間的函數關系;
(2)求當x為何值時y取得最大值,最大值是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2014年5月,我省南昌市遭受連日大暴雨天氣,某網站就“民眾是否支持加大修建城市地下排水設施的資金投入”進行投票,按照南昌暴雨前后兩個時間收集有效投票,暴雨后的投票收集了![]() 份,暴雨前的投票也收集了
份,暴雨前的投票也收集了![]() 份,所得統計結果如下表:
份,所得統計結果如下表:

已知工作人與從所有投票中任取一個,取到“不支持投入”的投票的概率為![]() .
.
(1)求列表中數據的值;
(2)能夠有多大的把握認為南昌暴雨對民眾是否贊成加大對修建城市地下排水設施的投入有關系?
附: 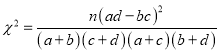
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() 的右焦點為F,右頂點為A,設離心率為e,且滿足
的右焦點為F,右頂點為A,設離心率為e,且滿足![]() ,其中O為坐標原點.
,其中O為坐標原點.
(Ⅰ)求橢圓C的方程;
(Ⅱ)過點![]() 的直線l與橢圓交于M,N兩點,求△OMN面積的最大值.
的直線l與橢圓交于M,N兩點,求△OMN面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=xlnx,g(x)=x3+ax2-x+2.
(Ⅰ)求函數f(x)的單調區間;
(Ⅱ)對任意x∈(0,+∞),![]() 恒成立,求實數a的取值范圍.
恒成立,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com