
【題目】已知 ![]() ,則導函數f′(x)是( )
,則導函數f′(x)是( )
A.僅有最小值的奇函數
B.既有最大值,又有最小值的偶函數
C.僅有最大值的偶函數
D.既有最大值,又有最小值的奇函數
【答案】D
【解析】解:f′(x)=x+sinx,令g(x)=x+sinx,則g′(x)=1+cosx.
當x∈[﹣1,1]時,g′(x)>0,所以f′(x)=g(x)在[﹣1,1]上單調遞增,
所以f′(﹣1)≤f′(x)≤f′(1),即﹣1﹣sin1≤f′(x)≤1+sin1.
又f′(﹣x)=﹣x+sin(﹣x)=﹣x﹣sinx=﹣(x+sinx)=﹣f′(x),所以f′(x)是奇函數.
故選D.
【考點精析】認真審題,首先需要了解函數的最大(小)值與導數(求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值).
比較,其中最大的是一個最大值,最小的是最小值).


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(1,sinx),
=(1,sinx), ![]() =(cos(2x+
=(cos(2x+ ![]() ),sinx),函數f(x)=
),sinx),函數f(x)= ![]()
![]() ﹣
﹣ ![]() cos2x
cos2x
(1)求函數f(x)的解析式及其單調遞增區間;
(2)當x∈[0, ![]() ]時,求函數f(x)的值域.
]時,求函數f(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程
的參數方程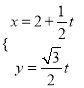 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點, ![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為:
的極坐標方程為: ![]() .
.
(1)把直線![]() 的參數方程化為極坐標方程,把曲線
的參數方程化為極坐標方程,把曲線![]() 的極坐標方程化為普通方程;
的極坐標方程化為普通方程;
(2)求直線![]() 與曲線
與曲線![]() 交點的極坐標(
交點的極坐標(![]() ≥0,0≤
≥0,0≤![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x3+ax2+bx+c,曲線y=f(x)在x=1處的切線為l:3x﹣y+1=0,當x= ![]() 時,y=f(x)有極值.
時,y=f(x)有極值.
(1)求a、b、c的值;
(2)求y=f(x)在[﹣3,1]上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若![]() 、
、![]() 是兩個相交平面,則在下列命題中,真命題的序號為( )
是兩個相交平面,則在下列命題中,真命題的序號為( )
①若直線![]() ,則在平面
,則在平面![]() 內一定不存在與直線
內一定不存在與直線![]() 平行的直線.
平行的直線.
②若直線![]() ,則在平面
,則在平面![]() 內一定存在無數條直線與直線
內一定存在無數條直線與直線![]() 垂直.
垂直.
③若直線![]() ,則在平面
,則在平面![]() 內不一定存在與直線
內不一定存在與直線![]() 垂直的直線.
垂直的直線.
④若直線![]() ,則在平面
,則在平面![]() 內一定存在與直線
內一定存在與直線![]() 垂直的直線.
垂直的直線.
A. ①③ B. ②③ C. ②④ D. ①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某花店每天以每枝![]() 元的價格從農場購進若干枝玫瑰花,然后以每枝
元的價格從農場購進若干枝玫瑰花,然后以每枝![]() 元的價格出售.如果當天賣不完,剩下的玫瑰花做垃圾處理.
元的價格出售.如果當天賣不完,剩下的玫瑰花做垃圾處理.
(1)若花店一天購進![]() 枝玫瑰花,求當天的利潤
枝玫瑰花,求當天的利潤![]() (單位:元)關于當天需求量
(單位:元)關于當天需求量![]() (單位:枝,
(單位:枝, ![]() )的函數解析式.
)的函數解析式.
(2)花店記錄了![]() 天玫瑰花的日需求量(單位:枝),整理得下表:
天玫瑰花的日需求量(單位:枝),整理得下表:
日需求量 |
|
|
|
|
|
|
|
頻數 |
|
|
|
|
|
|
|
假設花店在這![]() 天內每天購進
天內每天購進![]() 枝玫瑰花,求這
枝玫瑰花,求這![]() 天的日利潤(單位:元)的平均數.
天的日利潤(單位:元)的平均數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax+ ![]() +c是奇函數,且滿足f(1)=
+c是奇函數,且滿足f(1)= ![]() ,f(2)=
,f(2)= ![]() .
.
(1)求a,b,c的值;
(2)試判斷函數f(x)在區間(0, ![]() )上的單調性并證明.
)上的單調性并證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2cos2x+2 ![]() sinxcosx+a,且當
sinxcosx+a,且當 ![]() 時,f(x)的最小值為2.
時,f(x)的最小值為2.
(1)求a的值,并求f(x)的單調增區間;
(2)將函數y=f(x)的圖象上各點的縱坐標保持不變,橫坐標縮短到原來的 ![]() ,再把所得圖象向右平移
,再把所得圖象向右平移 ![]() 個單位,得到函數y=g(x),求方程g(x)=2在區間
個單位,得到函數y=g(x),求方程g(x)=2在區間 ![]() 上的所有根之和.
上的所有根之和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com