
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,左、右頂點分別為
,左、右頂點分別為![]() 、
、![]() ,線段
,線段![]() 的長為4.點
的長為4.點![]() 在橢圓
在橢圓![]() 上且位于第一象限,過點
上且位于第一象限,過點![]() ,
,![]() 分別作
分別作![]() ,
,![]() ,直線
,直線![]() ,
,![]() 交于點
交于點![]() .
.
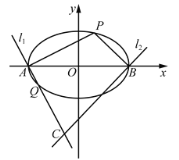
(1)若點![]() 的橫坐標為-1,求點
的橫坐標為-1,求點![]() 的坐標;
的坐標;
(2)直線![]() 與橢圓
與橢圓![]() 的另一交點為
的另一交點為![]() ,且
,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)先求出橢圓的方程,設直線![]() 的方程為
的方程為![]() .分別表示出直線
.分別表示出直線![]() 與
與![]() 的方程,聯立方程組,求出點
的方程,聯立方程組,求出點![]() 的坐標,利用點
的坐標,利用點![]() 的橫坐標為
的橫坐標為![]() ,求出
,求出![]() ,進而可求出點
,進而可求出點![]() 的坐標;(2 )聯立
的坐標;(2 )聯立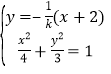 消去
消去![]() ,整理得
,整理得![]() ,求得
,求得![]() .由
.由![]() ,可得
,可得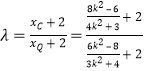
![]() ,結合
,結合![]() 即可求出
即可求出![]() 的取值范圍.
的取值范圍.
(1)設直線![]() 的斜率為
的斜率為![]() ,
,![]() ,
,
由題意得![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
所以橢圓![]() 的方程為
的方程為![]() .
.
因為點![]() 在橢圓
在橢圓![]() 上,且位于第一象限,
上,且位于第一象限,
所以![]() ,
,![]() ,直線
,直線![]() 的方程為
的方程為![]() .
.
因為![]() ,
,
所以![]() ,
,
所以直線![]() 的方程為
的方程為![]() .
.
聯立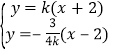 ,解得
,解得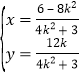 ,
,
即![]() .
.
因為![]() ,所以
,所以![]() ,
,
則直線![]() 的方程為
的方程為![]() .
.
因為![]() ,所以
,所以![]() .
.
則直線![]() 的方程為
的方程為![]() .
.
聯立 ,解得
,解得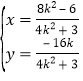 ,
,
即![]() .
.
因為點![]() 的橫坐標為-1,
的橫坐標為-1,
所以![]() ,解得
,解得![]() .
.
因為![]() ,
,
所以![]() .將
.將![]() 代入
代入![]() 可得,
可得,
點![]() 的坐標為
的坐標為![]() .
.
(2)設![]() ,
,![]() ,又直線
,又直線![]() 的方程為
的方程為![]() .
.
聯立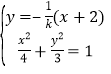 消去
消去![]() ,整理得
,整理得![]() ,
,
所以![]() ,
,
解得![]() .
.
因為![]() ,
,
所以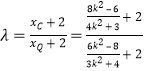
![]() .
.
因為![]() ,
,
所以![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】現有10名教師,其中男教師6名,女教師4名.
(1)現要從中選2名去參加會議,有多少種不同的選法?
(2)選出2名男教師或2名女教師去外地學習的選法有多少種?
(3)現要從中選出男、女老師各2名去參加會議,有多少種不同的選法?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年春節檔有多部優秀電影上映,其中《流浪地球》是比較火的一部.某影評網站統計了100名觀眾對《流浪地球》的評分情況,得到如下表格:
評價等級 | ★ | ★★ | ★★★ | ★★★★ | ★★★★★ |
分數 | 0~20 | 2140 | 4160 | 61~80 | 81100 |
人數 | 5 | 2 | 12 | 6 | 75 |
(1)根據以上評分情況,試估計觀眾對《流浪地球》的評價在四星以上(包括四星)的頻率;
(2)以表中各評價等級對應的頻率作為各評價等級對應的概率,假設每個觀眾的評分結果相互獨立.
(i)若從全國所有觀眾中隨機選取3名,求恰有2名評價為五星1名評價為一星的概率;
(ii)若從全國所有觀眾中隨機選取16名,記評價為五星的人數為X,求X的方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知甲箱中裝有3個紅球,2個黑球,乙箱中裝有2個紅球,3個黑球,這些球除顏色外完全相同,某商場舉行有獎促銷活動,規定顧客購物1000元以上,可以參與抽獎一次,設獎規則如下:每次分別從以上兩個箱子中各隨機摸出2個球,共4個球,若摸出4個球都是紅球,則獲得一等獎,獎金300元;摸出的球中有3個紅球,則獲得二等獎,獎金200元;摸出的球中有2個紅球,則獲得三等獎,獎金100元;其他情況不獲獎,每次摸球結束后將球放回原箱中.
(1)求在1次摸獎中,獲得二等獎的概率;
(2)若3人各參與摸獎1次,求獲獎人數X的數學期望![]() ;
;
(3)若商場同時還舉行打9折促銷活動,顧客只能在兩項促銷活動中任選一項參與.假若你購買了價值1200元的商品,那么你選擇參與哪一項活動對你有利?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的左右焦點分別為
的左右焦點分別為![]() ,
,![]() ,實軸長為6,漸近線方程為
,實軸長為6,漸近線方程為![]() ,動點
,動點![]() 在雙曲線左支上,點
在雙曲線左支上,點![]() 為圓
為圓![]() 上一點,則
上一點,則![]() 的最小值為
的最小值為
A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com