
【題目】已知數列![]() 為公差不為
為公差不為![]() 的等差數列,
的等差數列, ![]() 為前
為前![]() 項和,
項和, ![]() 和
和![]() 的等差中項為
的等差中項為![]() ,且
,且![]() .令
.令![]() 數列
數列![]() 的前
的前![]() 項和為
項和為![]() .
.
(1)求![]() 及
及![]() ;
;
(2)是否存在正整數![]() 成等比數列?若存在,求出所有的
成等比數列?若存在,求出所有的![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(Ⅰ)![]() ,
, ![]()
(Ⅱ)當![]() 可以使
可以使![]() 成等比數列.
成等比數列.
【解析】試題分析:(1)由于![]() 和
和![]() 的等差中項為
的等差中項為![]() ,可得
,可得![]() ,又
,又![]() .利用等差數列通項公式將其轉化為
.利用等差數列通項公式將其轉化為![]() 表示,解方程組求出其值,進而得到
表示,解方程組求出其值,進而得到![]() ,結合
,結合![]() 通項公式特點可采用裂項相消法求和
通項公式特點可采用裂項相消法求和![]() ;
;
(2)假設存在正整數m,n(1<m<n),使得T1,Tm,Tn成等比數列,則![]() ,當m=2時,化為
,當m=2時,化為![]() ,解得一組m,n的值滿足條件.當m≥3時,由于
,解得一組m,n的值滿足條件.當m≥3時,由于![]() 關于m單調遞增,可知
關于m單調遞增,可知![]() ,化為5n+27≤0,由于n>m>1,可知上式不成立
,化為5n+27≤0,由于n>m>1,可知上式不成立
試題解析:(Ⅰ)因為![]() 為等差數列,設公差為
為等差數列,設公差為![]() ,則由題意得
,則由題意得
![]()
整理得![]()
所以![]()
由![]()
所以![]()
(Ⅱ)假設存在
由(Ⅰ)知, ![]() ,所以
,所以![]()
若![]() 成等比,則有
成等比,則有
![]()
![]() ,(1)
,(1)
因為![]() ,所以
,所以![]() ,
,
因為![]() ,當
,當![]() 時,帶入(1)式,得
時,帶入(1)式,得![]() ;
;
綜上,當![]() 可以使
可以使![]() 成等比數列.
成等比數列.


科目:高中數學 來源: 題型:
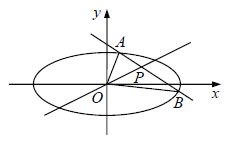
【題目】已知點![]() 在橢圓
在橢圓![]() 內,過
內,過![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于A,B兩點,且點
相交于A,B兩點,且點![]() 是線段AB的中點,O為坐標原點.
是線段AB的中點,O為坐標原點.
(Ⅰ)是否存在實數t,使直線![]() 和直線OP的傾斜角互補?若存在,求出
和直線OP的傾斜角互補?若存在,求出![]() 的值,若不存在,試說明理由;
的值,若不存在,試說明理由;
(Ⅱ)求![]() 面積S的最大值.
面積S的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2x+2﹣x ,
(1)判斷函數的奇偶性;
(2)用函數單調性定義證明:f(x)在(0,+∞)上為單調增函數;
(3)若f(x)=52﹣x+3,求x的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有一枚質地均勻的骰子,連續投擲兩次,計算:
(1)一共有多少種不同的結果?
(2)其中向上的點數之和是7的結果有多少種?
(3)向上的點數之和是7的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,將數字1,2,3,…, ![]() (
(![]() )全部填入一個2行
)全部填入一個2行![]() 列的表格中,每格填一個數字,第一行填入的數字依次為
列的表格中,每格填一個數字,第一行填入的數字依次為![]() ,
, ![]() ,…,
,…, ![]() ,第二行填入的數字依次為
,第二行填入的數字依次為![]() ,
, ![]() ,…,
,…, ![]() .記
.記![]() .
.

(Ⅰ)當![]() 時,若
時,若![]() ,
, ![]() ,
, ![]() ,寫出
,寫出![]() 的所有可能的取值;
的所有可能的取值;
(Ⅱ)給定正整數![]() .試給出
.試給出![]() ,
, ![]() ,…,
,…, ![]() 的一組取值,使得無論
的一組取值,使得無論![]() ,
, ![]() ,…,
,…, ![]() 填寫的順序如何,
填寫的順序如何, ![]() 都只有一個取值,并求出此時
都只有一個取值,并求出此時![]() 的值;
的值;
(Ⅲ)求證:對于給定的![]() 以及滿足條件的所有填法,
以及滿足條件的所有填法, ![]() 的所有取值的奇偶性相同.
的所有取值的奇偶性相同.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面給出了四個類比推理:
①![]() 為實數,若
為實數,若![]() 則
則![]() ;類比推出:
;類比推出: ![]() 為復數,若
為復數,若![]() 則
則![]() .
.
② 若數列![]() 是等差數列,
是等差數列, ![]() ,則數列
,則數列![]() 也是等差數列;類比推出:若數列
也是等差數列;類比推出:若數列![]() 是各項都為正數的等比數列,
是各項都為正數的等比數列, ![]() ,則數列
,則數列![]() 也是等比數列.
也是等比數列.
③ 若![]() 則
則![]() ; 類比推出:若
; 類比推出:若![]() 為三個向量,則
為三個向量,則![]() .
.
④ 若圓的半徑為![]() ,則圓的面積為
,則圓的面積為![]() ;類比推出:若橢圓的長半軸長為
;類比推出:若橢圓的長半軸長為![]() ,短半軸長為
,短半軸長為![]() ,則橢圓的面積為
,則橢圓的面積為![]() .上述四個推理中,結論正確的是( )
.上述四個推理中,結論正確的是( )
A. ① ② B. ② ③ C. ① ④ D. ② ④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com