【題目】如圖，將一個各面都涂了油漆的正方體，切割為125個同樣大小的小正方體，經過攪拌后，從中隨機取一個小正方體，記它的涂漆面數為X，則X的均值E（X）=（ ）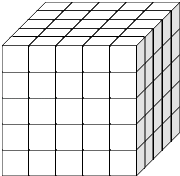
A.
B.
C.
D.
【答案】B
【解析】解：由題意可知：X所有可能取值為0，1，2，3．
①8個頂點處的8個小正方體涂有3面，∴P（X=3）= 
；
②每一條棱上除了兩個頂點處的小正方體，還剩下3個，一共有3×12=36個小正方體涂有2面，∴P（X=2）= 
；
③每個表面去掉四條棱上的16個小正方形，還剩下9個小正方形，因此一共有9×6=54個小正方體涂有一面，∴P（X=1）= 
．
④由以上可知：還剩下125﹣（8+36+54）=27個內部的小正方體的6個面都沒有涂油漆，∴P（X=0）= 
．
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
故X的分布列為
因此E（X）= 
= 
．
故選B．
由題意可知：X所有可能取值為0，1，2，3．①8個頂點處的8個小正方體涂有3面，②每一條棱上除了兩個頂點處的小正方體，還剩下3個，一共有3×12=36個小正方體涂有2面，
③每個表面去掉四條棱上的16個小正方形，還剩下9個小正方形，因此一共有9×6=54個小正方體涂有一面，④由以上可知：還剩下125﹣（8+36+54）=27個內部的小正方體的6個面都沒有涂油漆，根據上面的分析即可得出其概率及X的分布列，利用數學期望的計算公式即可得出．
科目：高中數學 來源： 題型：
【題目】已知函數
），記
的導函數為
.
（1） 證明：當
時， 
在
上的單調函數；
（2）若
在
處取得極小值，求
的取值范圍；
（3）設函數
的定義域為
，區間
.若
在
上是單調函數，則稱
在
上廣義單調.試證明函數
在
上廣義單調.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種出口產品的關稅稅率t．市場價格x(單位：千元)與市場供應量p(單位：萬件)之間近似滿足關系式：
，其中k．b均為常數．當關稅稅率為75%時，若市場價格為5千元，則市場供應量約為1萬件；若市場價格為7千元，則市場供應量約為2萬件．
(1)試確定k．b的值；
(2)市場需求量q(單位：萬件)與市場價格x近似滿足關系式：
．P = q時，市場價格稱為市場平衡價格．當市場平衡價格不超過4千元時，試確定關稅稅率
的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量 
=（ 
sinx，﹣1）， 
=（cosx，m），m∈R．
（1）若m= ，且 ∥ ，求 
的值；
（2）已知函數f（x）=2（ + ） ﹣2m2﹣1，若函數f（x）在[0， 
]上有零點，求m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有一解三角形的題目因紙張破損，有一條件不清，具體如下：在△ABC中，已知a= 
，2cos2 
=（ 
﹣1）cosB，c= ， 求角A，若該題的答案是A=60°，請將條件補充完整．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設f(n)是定義在N*上的增函數，f(4)＝5，且滿足：
①任意n∈N*，f(n)
Z；②任意m，n∈N*，有f(m)f(n)＝f(mn)＋f(m＋n－1)．
（1）求f(1)，f(2)，f(3)的值；
（2）求f(n)的表達式．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓心（a，b）（a＜0，b＜0）在直線y=2x+1上的圓，若其圓心到x軸的距離恰好等于圓的半徑，在y軸上截得的弦長為 
，則圓的方程為（ ）
A.（x+2）2+（y+3）2=9
B.（x+3）2+（y+5）2=25
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知F1、F2分別是雙曲線 
的左右焦點，A為雙曲線的右頂點，線段AF2的垂直平分線交雙曲線與P，且|PF1|=3|PF2|，則該雙曲線的離心率是（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com