【題目】已知
，函數(shù)
的最小值為1.
(1)求
的值；
(2)若
，求實數(shù)
的最大值.
【答案】（1）
（2）
【解析】【試題分析】（1）運用絕對值的三角不等式
或運用絕對值的定義將其化歸為分段函數(shù)的最值問題來處理，求解時借助分段函數(shù)的單調(diào)性可知
在
上單調(diào)遞減， 
在
上單調(diào)遞增，從而探求出
在
處取最小值；（2）先將不等式中的參數(shù)
分離出來得到
，再運用基本不等式或柯西不等式求
最值：
（1）法一： 
，
∵
且
，
∴
，當(dāng)
時取等號，即
的最小值為
，
∴
；
法二：∵
， ∴
，
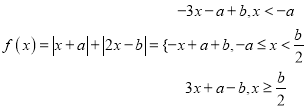顯然
在
上單調(diào)遞減， 
在
上單調(diào)遞增，
∴
的最小值為
， ∴
；
（2）法一：∵
恒成立，∴
恒成立，
，
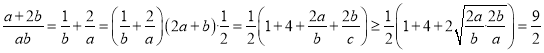當(dāng)
時， 
取得最小值
， ∴
，即實數(shù)
的最大值為
；
法二：∵
恒成立， ∴
恒成立， 
恒成立， 
， ∴
，即實數(shù)
的最大值為
．
閱讀快車系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】某高職院校進行自主招生文化素質(zhì)考試，考試內(nèi)容為語文、數(shù)學(xué)、英語三科，總分為200分.現(xiàn)從上線的考生中隨機抽取20人，將其成績用莖葉圖記錄如下：
男 | 女 | |||||||||||
15 | 6 | |||||||||||
5 | 4 | 16 | 3 | 5 | 8 | |||||||
8 | 2 | 17 | 2 | 3 | 6 | 8 | 8 | 8 | ||||
6 | 5 | 18 | 5 | 7 | ||||||||
19 | 2 | 3 | ||||||||||
（Ⅰ）計算上線考生中抽取的男生成績的方差
；（結(jié)果精確到小數(shù)點后一位）
（Ⅱ）從上述莖葉圖180分以上的考生中任選2人作為考生代表出席座談會，求所選考生恰為一男一女的概率.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】六個面都是平行四邊形的四棱柱稱為平行六面體．已知在平行四邊形ABCD中（如圖1），有AC2+BD2=2（AB2+AD2），則在平行六面體ABCD﹣A1B1C1D1中（如圖2），AC12+BD12+CA12+DB12等于（ ）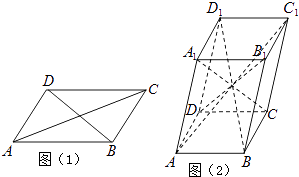 
A.2（AB2+AD2+AA12）
B.3（AB2+AD2+AA12）
C.4（AB2+AD2+AA12）
D.4（AB2+AD2）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知動點P（x，y）滿足方程xy=1（x＞0）．
（Ⅰ）求動點P到直線l：x+2y﹣ 
=0距離的最小值；
（Ⅱ）設(shè)定點A（a，a），若點P，A之間的最短距離為2 ，求滿足條件的實數(shù)a的取值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知拋物線C：y2=2px過點P（1，1）.過點（0，
）作直線l與拋物線C交于不同的兩點M，N，過點M作x軸的垂線分別與直線OP、ON交于點A，B，其中O為原點.
（Ⅰ）求拋物線C的方程，并求其焦點坐標(biāo)和準(zhǔn)線方程；
（Ⅱ）求證：A為線段BM的中點.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，DE∥BC，BC=2DE，CA⊥CB，CA⊥CD，CB⊥CD，F(xiàn)、G分別是AC、BC中點． 
（1）求證：平面DFG∥平面ABE；
（2）若AC=2BC=2CD=4，求二面角E﹣AB﹣C的正切值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在“一帶一路”的建設(shè)中，中石化集團獲得了某地深海油田區(qū)塊的開采權(quán)，集團在該地區(qū)隨機初步勘探了幾口井，取得了地質(zhì)資料.進入全面勘探時期后，集團按網(wǎng)絡(luò)點來布置井位進行全面勘探.由于勘探一口井的費用很高，如果新設(shè)計的井位與原有井位重合或接近，便利用舊井的地質(zhì)資料，不必打這口新井，以節(jié)約勘探費用.勘探初期數(shù)據(jù)資料下表：
井號I | 1 | 2 | 3 | 4 | 5 | 6 |
坐標(biāo) |
|
|
|
|
|
|
鉆探深度 | 2 | 4 | 5 | 6 | 8 | 10 |
出油量 | 40 | 70 | 110 | 90 | 160 | 205 |
（1）在散點圖中
號舊井位置大致分布在一條直線附近，借助前5組數(shù)據(jù)求得回歸線方程為
，求
，并估計
的預(yù)報值；
（2）現(xiàn)準(zhǔn)備勘探新井
，若通過1、3、5、7號井計算出的
的值（
精確到0.01）相比于（1）中
的值之差（即： 
）不超過10%，則使用位置最接近的已有舊井
，否則在新位置打井，請判斷可否使用舊井？（參考公式和計算結(jié)果：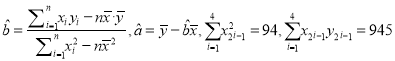 
）
（3）設(shè)出油量與鉆探深度的比值
不低于20的勘探井稱為優(yōu)質(zhì)井，在原有井號
的井中任意勘探3口井，求恰好2口是優(yōu)質(zhì)井的概率．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
的左、右焦點分別為
，橢圓
過點
，直線
交
軸于
，且
， 
為坐標(biāo)原點．
（1）求橢圓
的方程；
（2）設(shè)
是橢圓
的上頂點，過點
分別作直線
交橢圓
于
兩點，設(shè)這兩條直線的斜率分別為
，且
，證明：直線
過定點．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知數(shù)列{an}滿足：a1= 
，a2= 
，2an=an+1+an﹣1（n≥2，n∈N），數(shù)列{bn}滿足：b1＜0，3bn﹣bn﹣1=n（n≥2，n∈R），數(shù)列{bn}的前n項和為Sn ．
（1）求證：數(shù)列{bn﹣an}為等比數(shù)列；
（2）求證：數(shù)列{bn}為遞增數(shù)列；
（3）若當(dāng)且僅當(dāng)n=3時，Sn取得最小值，求b1的取值范圍．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
