
【題目】在三角形ABC中,![]() ,
,![]() ,
,![]() ,D是線段BC上一點,且
,D是線段BC上一點,且![]() ,F為線段AB上一點.
,F為線段AB上一點.
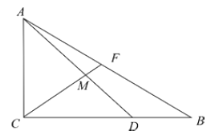
(1)若![]() ,求
,求![]() 的值;
的值;
(2)求![]() 的取值范圍;
的取值范圍;
(3)若![]() 為線段
為線段![]() 的中點,直線
的中點,直線![]() 與
與![]() 相交于點
相交于點![]() ,求
,求![]() .
.
 期末好成績系列答案
期末好成績系列答案 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優好卷系列答案
金狀元績優好卷系列答案科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的兩條漸近線與拋物線
的兩條漸近線與拋物線![]() 的準線分別交于A,B兩點,O為坐標原點,若
的準線分別交于A,B兩點,O為坐標原點,若![]() ,則雙曲線的離心率
,則雙曲線的離心率![]() __________.
__________.
【答案】![]()
【解析】因為雙曲線![]() 的兩條漸近線為
的兩條漸近線為![]() ,拋物線
,拋物線![]() 的準線為
的準線為![]() ,所以
,所以![]() ,
,
因此![]()
點睛:解決橢圓和雙曲線的離心率的求值及范圍問題其關鍵就是確立一個關于![]() 的方程或不等式,再根據
的方程或不等式,再根據![]() 的關系消掉
的關系消掉![]() 得到
得到![]() 的關系式,而建立關于
的關系式,而建立關于![]() 的方程或不等式,要充分利用橢圓和雙曲線的幾何性質、點的坐標的范圍等.
的方程或不等式,要充分利用橢圓和雙曲線的幾何性質、點的坐標的范圍等.
【題型】填空題
【結束】
16
【題目】若函數![]() 滿足:對于
滿足:對于![]() 圖象上任意一點P,在其圖象上總存在點
圖象上任意一點P,在其圖象上總存在點![]() ,使得
,使得![]() 成立,稱函數
成立,稱函數![]() 是“特殊對點函數”.給出下列五個函數:
是“特殊對點函數”.給出下列五個函數:
①![]() ;②
;②![]() (其中e為自然對數的底數);③
(其中e為自然對數的底數);③![]() ;④
;④![]() ;
;
⑤![]() .
.
其中是“特殊對點函數”的序號是__________.(寫出所有正確的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以
為參數),以![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸的極坐標系中,直線
軸的非負半軸為極軸的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,求
兩點,求![]() 的值.
的值.
【答案】(1)曲線![]() 的極坐標方程為:
的極坐標方程為: ![]() ;(2)6.
;(2)6.
【解析】試題分析:(1)先根據三角函數平方關系消參數得曲線![]() 的普通方程,再根據
的普通方程,再根據![]() 化為極坐標方程;(2)將直線l的極坐標方程代入曲線
化為極坐標方程;(2)將直線l的極坐標方程代入曲線![]() 的極坐標方程得
的極坐標方程得![]() ,再根據
,再根據![]() 求
求![]() 的值.
的值.
試題解析:解:(1)將方程![]() 消去參數
消去參數![]() 得
得![]() ,
,
∴曲線![]() 的普通方程為
的普通方程為![]() ,
,
將![]() 代入上式可得
代入上式可得![]() ,
,
∴曲線![]() 的極坐標方程為:
的極坐標方程為: ![]() . -
. -
(2)設![]() 兩點的極坐標方程分別為
兩點的極坐標方程分別為![]() ,
,
由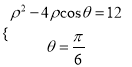 消去
消去![]() 得
得![]() ,
,
根據題意可得![]() 是方程
是方程![]() 的兩根,
的兩根,
∴![]() ,
,
∴![]() .
.
【題型】解答題
【結束】
23
【題目】選修4—5:不等式選講
已知函數![]() .
.
(1)當![]() 時,求關于x的不等式
時,求關于x的不等式![]() 的解集;
的解集;
(2)若關于x的不等式![]() 有解,求a的取值范圍.
有解,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠用7萬元錢購買了一臺新機器,運輸安裝費用2千元,每年投保、動力消耗的費用也為2千元,每年的保養、維修、更換易損零件的費用逐年增加,第一年為2千元,第二年為3千元,第三年為4千元,依此類推,即每年增加1千元.
(1)求使用n年后,保養、維修、更換易損零件的累計費用S(千元)關于n的表達式;
(2)問這臺機器最佳使用年限是多少年?并求出年平均費用(單位:千元)的最小值.(最佳使用年限是指使年平均費用最小的時間,年平均費用=(購入機器費用+運輸安裝費用+每年投保、動力消耗的費用+保養、維修、更換易損零件的累計費用)÷機器使用的年數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過原點的一條直線與橢圓![]() =1(a>b>0)交于A,B兩點,以線段AB為直徑的圓過該橢圓的右焦點F2,若∠ABF2∈[
=1(a>b>0)交于A,B兩點,以線段AB為直徑的圓過該橢圓的右焦點F2,若∠ABF2∈[![]() ],則該橢圓離心率的取值范圍為( )
],則該橢圓離心率的取值范圍為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com