
【題目】已知![]() 分別是橢圓
分別是橢圓![]() 的左、右焦點,離心率為
的左、右焦點,離心率為![]() ,
, ![]() 分別是橢圓的上、下頂點,
分別是橢圓的上、下頂點, ![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于相異兩點
交于相異兩點![]() ,且滿足直線
,且滿足直線![]() 的斜率之積為
的斜率之積為![]() ,證明:直線
,證明:直線![]() 恒過定點,并采定點的坐標(biāo).
恒過定點,并采定點的坐標(biāo).
【答案】(1)![]() (2)直線
(2)直線![]() 恒過定點
恒過定點![]() .
.
【解析】試題分析:(1)設(shè)出相關(guān)點坐標(biāo),利用![]() 和離心率為
和離心率為![]() 得到幾何元素間的關(guān)系即可求解;(2)聯(lián)立直線和橢圓的方程,得到關(guān)于
得到幾何元素間的關(guān)系即可求解;(2)聯(lián)立直線和橢圓的方程,得到關(guān)于![]() 的一元二次方程,利用根與系數(shù)的關(guān)系、斜率公式得到等式,進(jìn)而利用直線方程判定其過定點.
的一元二次方程,利用根與系數(shù)的關(guān)系、斜率公式得到等式,進(jìn)而利用直線方程判定其過定點.
試題解析:(1)由題知![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,![]() .
.
∴![]() ①
①
由![]() ,得
,得![]() ② 又
② 又![]() ③
③
由①②③聯(lián)立解得:![]()
∴橢圓![]() 的方程為
的方程為![]() .
.
(2)證明:由橢圓![]() 的方程得,上頂點
的方程得,上頂點![]() ,
,
設(shè)![]() ,
,![]() ,由題意知,
,由題意知,![]()
由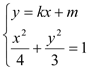 得:
得:![]()
∴![]() ,
,
又,
![]() ,
,
由![]() ,得
,得![]() ,
,
即:![]() ,
,
∴![]() ,
,
化簡得:![]()
解得:![]() ,結(jié)合
,結(jié)合![]() 知
知![]() ,
,
即直線![]() 恒過定點
恒過定點![]() .
.


 通城學(xué)典默寫能手系列答案
通城學(xué)典默寫能手系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)是定義在R上的奇函數(shù),當(dāng)x≥0時,f(x)=x2-2x.
(1)求f(x)的解析式,并畫出f(x)的圖象;
(2)設(shè)g(x)=f(x)-k,利用圖象討論:當(dāng)實數(shù)k為何值時,函數(shù)g(x)有一個零點?二個零點?三個零點?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓C:x2+y2=12,直線l:4x+3y=25,設(shè)點A是圓C上任意一點,求點A到直線l的距離小于2的概率.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在某地區(qū)某高傳染性病毒流行期間,為了建立指標(biāo)顯示疫情已受控制,以便向該地區(qū)居眾顯示可以過正常生活,有公共衛(wèi)生專家建議的指標(biāo)是“連續(xù)7天每天新增感染人數(shù)不超過5人”,根據(jù)連續(xù)7天的新增病例數(shù)計算,下列① ~ ⑤各個選項中,一定符合上述指標(biāo)的是 ( )
①平均數(shù)![]() ; ②標(biāo)準(zhǔn)差
; ②標(biāo)準(zhǔn)差![]() ; ③平均數(shù)
; ③平均數(shù)![]() 且標(biāo)準(zhǔn)差
且標(biāo)準(zhǔn)差![]() ;
;
④平均數(shù)![]() 且極差小于或等于2;⑤眾數(shù)等于1且極差小于或等于4。
且極差小于或等于2;⑤眾數(shù)等于1且極差小于或等于4。
A. ①② B. ③④ C. ③④⑤ D. ④⑤
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖, ![]() 分別是橢圓
分別是橢圓![]() 的左、右焦點,
的左、右焦點, ![]() 是橢圓
是橢圓![]() 的頂點,
的頂點, ![]() 是直線
是直線![]() 與橢圓
與橢圓![]() 的另一個交點,
的另一個交點, ![]() .
.

(1)求橢圓![]() 的離心率;
的離心率;
(2)已知![]() 的面積為
的面積為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直線l:3x-y-1=0上求點P和Q,使得
(1)點P到點A(4,1)和B(0,4)的距離之差最大;
(2)點Q到點A(4,1)和C(3,4)的距離之和最小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}的前n項Sn=(﹣1)n ![]() ,若存在正整數(shù)n,使得(an﹣1﹣p)(an﹣p)<0成立,則實數(shù)p的取值范圍是 .
,若存在正整數(shù)n,使得(an﹣1﹣p)(an﹣p)<0成立,則實數(shù)p的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=﹣ ![]() x3+
x3+ ![]() x2﹣2x(a∈R)
x2﹣2x(a∈R)
(1)當(dāng)a=3時,求函數(shù)f(x)的單調(diào)區(qū)間;
(2)若對于任意x∈[1,+∞)都有f′(x)<2(a﹣1)成立,求實數(shù)a的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com