
【題目】若| ![]() |=1,|
|=1,| ![]() |=m,|
|=m,| ![]() +
+ ![]() |=2.
|=2.
(1)若| ![]() +2
+2 ![]() |=3,求實數m的值;
|=3,求實數m的值;
(2)若 ![]() +
+ ![]() 與
與 ![]() ﹣
﹣ ![]() 的夾角為
的夾角為 ![]() ,求實數m的值.
,求實數m的值.
【答案】
(1)證明:因為| ![]() +
+ ![]() |=2,所以|
|=2,所以| ![]() +
+ ![]() |2=4.
|2=4.
即以 ![]() 2+
2+ ![]() 2+2
2+2 ![]()
![]() =4.,
=4.,
又| ![]() |=1,|
|=1,| ![]() |=m,所以
|=m,所以 ![]() .
.
由| ![]() +2
+2 ![]() |=3,所以所以|
|=3,所以所以| ![]() +2
+2 ![]() |2=9.
|2=9.
即以 ![]() 2+4
2+4 ![]() 2+4
2+4 ![]()
![]() =9,
=9,
所以1+4× ![]() +4m2=9,解得m=±1,
+4m2=9,解得m=±1,
又| ![]() |≥0,所以m=1.
|≥0,所以m=1.
(2)證明:因為,| ![]() |=1,|
|=1,| ![]() |=m,
|=m, ![]()
所以| ![]() ﹣
﹣ ![]() |2=
|2= ![]() 2+
2+ ![]() 2﹣2
2﹣2 ![]()
![]() =1﹣2×
=1﹣2× ![]() +m2=2m2﹣2,|
+m2=2m2﹣2,| ![]() ﹣
﹣ ![]() |=
|= ![]() .
.
又因為 ![]() +
+ ![]() 與
與 ![]() ﹣
﹣ ![]() 的夾角為
的夾角為 ![]() ,所以(
,所以( ![]() +
+ ![]() )(
)( ![]() ﹣
﹣ ![]() )=以
)=以 ![]() 2﹣
2﹣ ![]() 2=|
2=| ![]() +
+ ![]() |×|
|×| ![]() ﹣
﹣ ![]() |cos
|cos ![]()
即,所以1﹣m2=2× ![]() ,解得m=±
,解得m=± ![]() ,
,
又| ![]() |≥0,所以m=
|≥0,所以m= ![]() .
.
【解析】(1)由| ![]() +
+ ![]() |=2,|
|=2,| ![]() +2
+2 ![]() |=3
|=3 ![]() 2+
2+ ![]() 2+2
2+2 ![]()
![]() =4 和
=4 和 ![]() 2+4
2+4 ![]() 2+4
2+4 ![]()
![]() =9,即可求解;(2)利用(
=9,即可求解;(2)利用( ![]() +
+ ![]() )(
)( ![]() ﹣
﹣ ![]() )=以
)=以 ![]() 2﹣
2﹣ ![]() 2=|
2=| ![]() +
+ ![]() |×|
|×| ![]() ﹣
﹣ ![]() |cos
|cos ![]() 求解.
求解.


科目:高中數學 來源: 題型:
【題目】分別求出適合下列條件的直線方程: (Ⅰ)經過點P(﹣3,2)且在x軸上的截距等于在y軸上截距的2倍;
(Ⅱ)經過直線2x+7y﹣4=0與7x﹣21y﹣1=0的交點,且和A(﹣3,1),B(5,7)等距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司擬設計一個扇環形狀的花壇(如圖所示),該扇環是由以點O為圓心的兩個同心圓弧和延長后通過點AD的兩條線段圍成.設圓弧 ![]() 、
、 ![]() 所在圓的半徑分別為f(x)、R米,圓心角為θ(弧度).
所在圓的半徑分別為f(x)、R米,圓心角為θ(弧度). 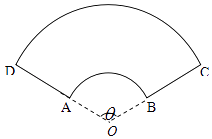
(1)若θ= ![]() ,r1=3,r2=6,求花壇的面積;
,r1=3,r2=6,求花壇的面積;
(2)設計時需要考慮花壇邊緣(實線部分)的裝飾問題,已知直線部分的裝飾費用為60元/米,弧線部分的裝飾費用為90元/米,預算費用總計1200元,問線段AD的長度為多少時,花壇的面積最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三棱錐P﹣ABC,底面ABC為邊長為2 ![]() 的正三角形,平面PBC⊥平面ABC,PB=PC=2,D為AP上一點,AD=2DP,O為底面三角形中心.
的正三角形,平面PBC⊥平面ABC,PB=PC=2,D為AP上一點,AD=2DP,O為底面三角形中心. 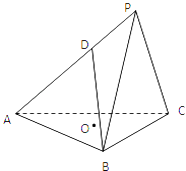
(1)求證DO∥面PBC;
(2)求證:BD⊥AC;
(3)設M為PC中點,求平面MBD和平面BDO所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|f(x)=lg(x﹣1)+ ![]() },集合B={y|y=2x+a,x≤0}.
},集合B={y|y=2x+a,x≤0}.
(1)若a= ![]() ,求A∪B;
,求A∪B;
(2)若A∩B=,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點F1 , F2分別是雙曲線 ![]() 的左、右焦點,過F1且垂直于x軸的直線與雙曲線交于A,B兩點,若△ABF2是銳角三角形,則該雙曲線離心率的取值范圍是( )
的左、右焦點,過F1且垂直于x軸的直線與雙曲線交于A,B兩點,若△ABF2是銳角三角形,則該雙曲線離心率的取值范圍是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學在利用“五點法”作函數f(x)=Asin(ωx+)+t(其中A>0, ![]() )的圖象時,列出了如表格中的部分數據.
)的圖象時,列出了如表格中的部分數據.
x |
|
|
|
|
|
ωx+ | 0 | | π | | 2π |
f(x) | 2 | 6 | 2 | ﹣2 | 2 |
(1)請將表格補充完整,并寫出f(x)的解析式.
(2)若 ![]() ,求f(x)的最大值與最小值.
,求f(x)的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知y=f(x)是定義在R上的奇函數,當x≥0時,f(x)=x+x2 .
(1)求x<0時,f(x)的解析式;
(2)問是否存在這樣的非負數a,b,當x∈[a,b]時,f(x)的值域為[4a﹣2,6b﹣6]?若存在,求出所有的a,b值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com