
【題目】設![]() ,函數
,函數![]() ,
,![]() 是函數
是函數![]() 的導函數,
的導函數, ![]() 是自然對數的底數.
是自然對數的底數.
(1)當![]() 時,求導函數
時,求導函數![]() 的最小值;
的最小值;
(2)若不等式![]() 對任意
對任意![]() 恒成立,求實數
恒成立,求實數![]() 的最大值;
的最大值;
(3)若函數![]() 存在極大值與極小值,求實數
存在極大值與極小值,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】分析:(1)先求導數,再求導函數的導數為![]() ,求零點,列表分析導函數單調性變化規律,進而確定導函數最小值取法,(2)先變量分離化簡不等式
,求零點,列表分析導函數單調性變化規律,進而確定導函數最小值取法,(2)先變量分離化簡不等式![]() ,再利用導數研究
,再利用導數研究![]() 單調性,根據單調性確定其最小值,即得實數
單調性,根據單調性確定其最小值,即得實數![]() 的取值范圍,進而得其最大值;(3)函數
的取值范圍,進而得其最大值;(3)函數![]() 存在極大值與極小值,即
存在極大值與極小值,即![]() 存在兩個零點,且在零點的兩側異號.先確定導函數
存在兩個零點,且在零點的兩側異號.先確定導函數![]() 不單調且最小值小于零,即得
不單調且最小值小于零,即得![]() ,再證明
,再證明![]() 時
時![]() 有且僅有兩個零點.
有且僅有兩個零點.
詳解:解:![]()
(1)當![]() 時,
時,![]() 記
記![]()
則![]() ,由
,由![]() 得
得![]() .
.
當![]() 時,
時,![]() ,
,![]() 單調遞減
單調遞減
當![]() 時,
時,![]() ,
,![]() 單調遞增
單調遞增
所以當![]() 時,
時,![]()
所以![]()
(2)由![]() 得
得![]() ,即
,即![]()
因為![]() ,所以
,所以![]() .
.
記![]() ,則
,則![]()
![]()
記![]() ,則
,則![]()
![]()
因為![]() ,所以
,所以![]() 且不恒為0
且不恒為0
所以![]() 時,
時,![]() 單調遞增,
單調遞增,
當![]() 時,
時,![]() ,所以
,所以![]()
所以![]() 在
在![]() 上單調遞增,
上單調遞增,![]()
因為![]() 對
對![]() 恒成立,
恒成立,
所以![]() ,即
,即![]()
所以實數![]() 的最大值為
的最大值為![]()
(3)記![]() ,
,![]()
因為![]() 存在極大值與極小值,
存在極大值與極小值,
所以![]() ,即
,即![]() 存在兩個零點,且
存在兩個零點,且![]() 在零點的兩側異號.
在零點的兩側異號.
①當![]() 時,
時,![]() ,
,![]() 單調遞增,
單調遞增,
此時![]() 不存在兩個零點;
不存在兩個零點;
②當![]() 時,由
時,由![]() ,得
,得![]()
當![]() 時,
時,![]() ,
,![]() 單調遞減,
單調遞減,
當![]() 時,
時,![]() ,
,![]() 單調遞增,
單調遞增,
所以![]()
![]()
所以![]() 存在兩個零點的必要條件為:
存在兩個零點的必要條件為:![]()
![]() ,即
,即![]()
由![]() 時,
時,
(ⅰ)記![]() ,則
,則![]()
所以當![]() 時,
時,![]() 單調遞減,
單調遞減,
當![]() 時,
時,![]() ,所以
,所以![]() .
.
所以![]() 在
在![]() 上,有且只有一個零點.
上,有且只有一個零點.
又![]() 在
在![]() 上單調,
上單調,
所以![]() 在
在![]() 上有且只有一個零點,記為
上有且只有一個零點,記為![]() ,
,
由![]() 在
在![]() 內單調遞減,易得當
內單調遞減,易得當![]() 時,函數
時,函數![]() 存在極大值
存在極大值
(ⅱ)記![]() ,則
,則![]()
所以![]() 時,
時,![]() ,所以
,所以![]()
由(1)知![]() 時,
時,![]() 有
有![]()
所以![]() 在
在![]() 上單調遞增,所以
上單調遞增,所以![]() 時,
時, ![]()
因為![]() 且
且![]() ,
,![]() 的圖像在
的圖像在![]() 單調且不間斷,
單調且不間斷,
所以![]() 在
在![]() 上,有且只有一個零點.
上,有且只有一個零點.
又![]() 在
在![]() 上單調
上單調
所以![]() 在
在![]() 上有且只有一個零點,記為
上有且只有一個零點,記為![]() ,
,
由![]() 在
在![]() 內單調遞增,易得當
內單調遞增,易得當![]() 時,函數
時,函數![]() 存在極小值
存在極小值
綜上,實數![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數f(x),g(x)滿足關系g(x)=f(x)f(x+α),其中α是常數.
(1)設f(x)=cosx+sinx,![]() ,求g(x)的解析式;
,求g(x)的解析式;
(2)設計一個函數f(x)及一個α的值,使得![]() ;
;
(3)當f(x)=|sinx|+cosx,![]() 時,存在x1,x2∈R,對任意x∈R,g(x1)≤g(x)≤g(x2)恒成立,求|x1-x2|的最小值.
時,存在x1,x2∈R,對任意x∈R,g(x1)≤g(x)≤g(x2)恒成立,求|x1-x2|的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三名工人加工同一種零件,他們在一天中的工作情況如圖所示,其中Ai的橫、縱坐標分別為第i名工人上午的工作時間和加工的零件數,點Bi的橫、縱坐標分別為第i名工人下午的工作時間和加工的零件數,i=1,2,3.
①記Qi為第i名工人在這一天中加工的零件總數,則Q1 , Q2 , Q3中最大的是 .
②記pi為第i名工人在這一天中平均每小時加工的零件數,則p1 , p2 , p3中最大的是 . 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市要對該市六年級學生進行體育素質調查測試,現讓學生從“跳繩、短跑![]() 米、長跑
米、長跑![]() 米、仰臥起坐、游泳
米、仰臥起坐、游泳![]() 米、立定跳遠”
米、立定跳遠”![]() 項中選擇
項中選擇![]() 項進行測試,其中“短跑、長跑、仰臥起坐”
項進行測試,其中“短跑、長跑、仰臥起坐”![]() 項中至少選擇其中
項中至少選擇其中![]() 項進行測試.現從該市六年級學生中隨機抽取了
項進行測試.現從該市六年級學生中隨機抽取了![]() 名學生進行調查,他們選擇的項目中包含“短跑、長跑、仰臥起坐”的項目個數及人數統計如下表:(其中
名學生進行調查,他們選擇的項目中包含“短跑、長跑、仰臥起坐”的項目個數及人數統計如下表:(其中![]() )
)
選擇的項目中包含“短跑、長跑、仰臥起坐”的項目個數 |
|
|
|
人數 |
|
|
|
已知從所調查的![]() 名學生中任選
名學生中任選![]() 名,他們選擇“短跑、長跑、仰臥起坐”的項目個數不相等概率為
名,他們選擇“短跑、長跑、仰臥起坐”的項目個數不相等概率為![]() ,記
,記![]() 為這
為這![]() 名學生選擇“短跑、長跑、仰臥起坐”的項目個數之和.
名學生選擇“短跑、長跑、仰臥起坐”的項目個數之和.
(1)求![]() 的值;
的值;
(2)求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年2月22日,在韓國平昌冬奧會短道速滑男子500米比賽中,中國選手武大靖以連續打破世界紀錄的優異表現,為中國代表隊奪得了本屆冬奧會的首枚金牌,也創造中國男子冰上競速項目在冬奧會金牌零的突破.某高校為調查該校學生在冬奧會期間累計觀看冬奧會的時間情況,收集了200位男生、100位女生累計觀看冬奧會時間的樣本數據(單位:小時).又在100位女生中隨機抽取20個人,已知這20位女生的數據莖葉圖如圖所示.
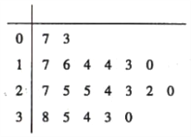

(I)將這20位女生的時間數據分成8組,分組區間分別為![]()
![]() ,
,![]() ,…,
,…,![]() ,
,![]()
![]() ,完成頻率分布直方圖;
,完成頻率分布直方圖;
(II)以(I)中的頻率作為概率,求1名女生觀看冬奧會時間不少于30小時的概率;(III)以(I)中的頻率估計100位女生中累計觀看時間小于20個小時的人數,已知200位男生中累計觀看時間小于20小時的男生有50人.請完成下面的列聯表,并判斷是否有99%的把握認為“該校學生觀看冬奧會累計時間與性別有關”.
男生 | 女生 |
| |
累計觀看時間小于20小時 | |||
累計觀看時間小于20小時 | |||
總計 | 300 |
附:(![]()
![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】雙曲線E: ![]() =1(a>0,b>0)的左、右焦點分別為F1、F2 , P是E坐支上一點,且|PF1|=|F1F2|,直線PF2與圓x2+y2=a2相切,則E的離心率為 .
=1(a>0,b>0)的左、右焦點分別為F1、F2 , P是E坐支上一點,且|PF1|=|F1F2|,直線PF2與圓x2+y2=a2相切,則E的離心率為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高一(1)班參加校生物競賽學生的成績的莖葉圖和頻率分布直方圖都受到不同程度的破壞,但可見部分如下,據此解答如下問題:

(1)求高一(1)班參加校生物競賽的人數及分數在[80,90)之間的頻數,并計算頻率分布直方圖中[80,90)間的矩形的高;
(2)若要從分數在[80,100]之間的學生中任選2人進行某項研究,求至少有1人分數在[90,100]之間的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC﹣A1B1C1中,AC=AA1=2,AB=BC=2 ![]() ,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1與A1C相交于點D.
,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1與A1C相交于點D. 
(1)求證:BC1⊥平面AA1C1C;
(2)求二面角C1﹣AB﹣C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,以原點O為極點,x軸的非負半軸為極軸,建立極坐標系,若直線l的參數方程為 ![]() (t為參數,α為l的傾斜角),曲線E的極坐標方程為ρ=4sinθ.射線θ=β,θ=β+
(t為參數,α為l的傾斜角),曲線E的極坐標方程為ρ=4sinθ.射線θ=β,θ=β+ ![]() ,θ=β﹣
,θ=β﹣ ![]() 與曲線E分別交于不同于極點的三點A、B、C.
與曲線E分別交于不同于極點的三點A、B、C.
(1)求證:|OB|+|OC|= ![]() |OA|;
|OA|;
(2)當β= ![]() 時,直線l過B、C兩點,求y0與α的值.
時,直線l過B、C兩點,求y0與α的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com