
【題目】已知數(shù)列![]() 的前n項(xiàng)的和Sn,點(diǎn)(n,Sn)在函數(shù)
的前n項(xiàng)的和Sn,點(diǎn)(n,Sn)在函數(shù)![]() =2x2+4x圖象上:
=2x2+4x圖象上:
(1)證明![]() 是等差數(shù)列;
是等差數(shù)列;
(2)若函數(shù)![]() ,數(shù)列{bn}滿足bn=
,數(shù)列{bn}滿足bn=![]() ,記cn=anbn,求數(shù)列
,記cn=anbn,求數(shù)列![]() 前n項(xiàng)和Tn;
前n項(xiàng)和Tn;
(3)是否存在實(shí)數(shù)λ,使得當(dāng)x≤λ時(shí),f(x)=﹣x2+4x﹣![]() ≤0對(duì)任意n∈N*恒成立?若存在,求出最大的實(shí)數(shù)λ,若不存在,說(shuō)明理由.
≤0對(duì)任意n∈N*恒成立?若存在,求出最大的實(shí)數(shù)λ,若不存在,說(shuō)明理由.
【答案】(1) 數(shù)列{an}的通項(xiàng)公式為an=4n+2;(2) Tn=10﹣(2n+5)![]() ;(3) 實(shí)數(shù)λ=1,見(jiàn)解析.
;(3) 實(shí)數(shù)λ=1,見(jiàn)解析.
【解析】試題分析:(1)要求數(shù)列的通項(xiàng)公式,利用![]() ,然后把
,然后把![]() 代入驗(yàn)證;
代入驗(yàn)證;
(2)由函數(shù)![]() ,數(shù)列
,數(shù)列![]() 滿足
滿足![]() ,利用錯(cuò)位相減法可得數(shù)列{
,利用錯(cuò)位相減法可得數(shù)列{![]() 前
前![]() 項(xiàng)和
項(xiàng)和![]()
(3)假設(shè)存在實(shí)數(shù)![]() ,使得當(dāng)
,使得當(dāng)![]() 時(shí),
時(shí),![]()
對(duì)任意![]() 恒成立,即
恒成立,即![]() 對(duì)任意
對(duì)任意![]() 恒成立,由
恒成立,由![]()
是遞增數(shù)列,能推導(dǎo)出存在最大的實(shí)數(shù)![]() ,使得當(dāng)
,使得當(dāng)![]() 時(shí),
時(shí),![]() 對(duì)任意
對(duì)任意![]() 恒成立
恒成立
試題解析;(1)由題意,Sn=2n2+4n,
當(dāng)n=1時(shí),a1=S1=6,
![]() n≥2時(shí),an=Sn﹣Sn﹣1=(2n2+4n)﹣[2(n﹣1)2+4(n﹣1)]=4n+2,
n≥2時(shí),an=Sn﹣Sn﹣1=(2n2+4n)﹣[2(n﹣1)2+4(n﹣1)]=4n+2,
當(dāng)n=1時(shí),a1=S1=4+2=6,也適合上式
∴數(shù)列{an}的通項(xiàng)公式為an=4n+2,n∈N*;![]() 是等差數(shù)列
是等差數(shù)列
(2)∵函數(shù)g(x)=2﹣x,
∴數(shù)列{bn}滿足bn=g(n)=2﹣n,
又∵cn=anbn,
∴Tn=6×2﹣1+10×2﹣2+14×2﹣3+…+(4n+2)×2﹣n,…①,
∴![]() Tn=6×2﹣2+10×2﹣3+…+(4n﹣2)×2﹣n+(4n+2)×2﹣(n+1),…②,
Tn=6×2﹣2+10×2﹣3+…+(4n﹣2)×2﹣n+(4n+2)×2﹣(n+1),…②,
①﹣②得:
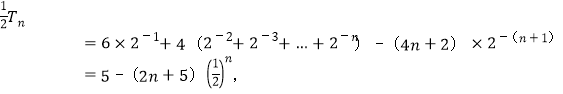
![]()
(3)假設(shè)存在實(shí)數(shù)λ,使得當(dāng)x≤λ時(shí),![]() 對(duì)任意
對(duì)任意
n∈N*恒成立,即![]() 任意n∈N*恒成立,
任意n∈N*恒成立,
∵an=4n+2,![]() 是遞增數(shù)列,
是遞增數(shù)列,
所以只要﹣x2+4x≤c1,即x2﹣4x+3≥0,解得x≤1或x≥3.
所以存在最大的實(shí)數(shù)λ=1,使得當(dāng)x≤λ時(shí),f(x)≤cn對(duì)任意n∈N*恒成立.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知各項(xiàng)均為正數(shù)的等比數(shù)列{an}中,a2=4,a4=16.
(1)求公比q;
(2)若a3 , a5分別為等差數(shù)列{bn}的第3項(xiàng)和第5項(xiàng),求數(shù)列{bn}的通項(xiàng)公式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
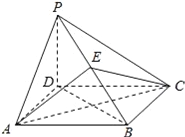
【題目】如圖,四棱錐P﹣ABCD的底面是正方形,PD⊥底面ABCD,點(diǎn)E在棱PB上.
(1)求證:平面AEC⊥平面PDB;
(2)當(dāng)PD=![]() AB,且E為PB的中點(diǎn)時(shí),求AE與平面PDB所成的角的大小.
AB,且E為PB的中點(diǎn)時(shí),求AE與平面PDB所成的角的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知a<0,函數(shù)f(x)=acosx+ ![]() +
+ ![]() ,其中x∈[﹣
,其中x∈[﹣ ![]() ,
, ![]() ].
].
(1)設(shè)t= ![]() +
+ ![]() ,求t的取值范圍,并把f(x)表示為t的函數(shù)g(t);
,求t的取值范圍,并把f(x)表示為t的函數(shù)g(t);
(2)求函數(shù)f(x)的最大值(可以用a表示);
(3)若對(duì)區(qū)間[﹣ ![]() ,
, ![]() ]內(nèi)的任意x1 , x2 , 總有|f(x1)﹣f(x2)|≤1,求實(shí)數(shù)a的取值范圍.
]內(nèi)的任意x1 , x2 , 總有|f(x1)﹣f(x2)|≤1,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)M=( ![]() ﹣1)(
﹣1)( ![]() ﹣1)(
﹣1)( ![]() ﹣1)滿足a+b+c=1(其中a>0,b>0,c>0),則M的取值范圍是( )
﹣1)滿足a+b+c=1(其中a>0,b>0,c>0),則M的取值范圍是( )
A.[0, ![]() )
)
B.[ ![]() ,1)
,1)
C.[1,8)
D.[8,+∞)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在ABC中,內(nèi)角A,B,C的對(duì)邊分別為a,b,c,已知 ![]()
(1)求 ![]() 的值;
的值;
(2)若 ![]() ,b=2,求△ABC的面積S.
,b=2,求△ABC的面積S.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知 ![]() =(2,1),
=(2,1), ![]() =(1,7),
=(1,7), ![]() =(5,1),設(shè)R是直線OP上的一點(diǎn),其中O是坐標(biāo)原點(diǎn).
=(5,1),設(shè)R是直線OP上的一點(diǎn),其中O是坐標(biāo)原點(diǎn).
(1)求使 ![]() 取得最小值時(shí)
取得最小值時(shí) ![]() 的坐標(biāo)的坐標(biāo);
的坐標(biāo)的坐標(biāo);
(2)對(duì)于(1)中的點(diǎn)R,求 ![]() 與
與 ![]() 夾角的余弦值.
夾角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】交強(qiáng)險(xiǎn)是車(chē)主必須為機(jī)動(dòng)車(chē)購(gòu)買(mǎi)的險(xiǎn)種,若普通6座以下私家車(chē)投保交強(qiáng)險(xiǎn)第一年的費(fèi)用(基準(zhǔn)保費(fèi))統(tǒng)一為![]() 元,在下一年續(xù)保時(shí),實(shí)行的是費(fèi)率浮動(dòng)機(jī)制,保費(fèi)與上一年度車(chē)輛發(fā)生道路交通事故的情況相聯(lián)系,發(fā)生交通事故的次數(shù)越多,費(fèi)率也就越高,具體浮動(dòng)情況如下表:
元,在下一年續(xù)保時(shí),實(shí)行的是費(fèi)率浮動(dòng)機(jī)制,保費(fèi)與上一年度車(chē)輛發(fā)生道路交通事故的情況相聯(lián)系,發(fā)生交通事故的次數(shù)越多,費(fèi)率也就越高,具體浮動(dòng)情況如下表:
交強(qiáng)險(xiǎn)浮動(dòng)因素和浮動(dòng)費(fèi)率比率表 | ||
浮動(dòng)因素 | 浮動(dòng)比率 | |
| 上一個(gè)年度未發(fā)生有責(zé)任道路交通事故 | 下浮10% |
| 上兩個(gè)年度未發(fā)生責(zé)任道路交通事故 | 下浮20% |
| 上三個(gè)及以上年度未發(fā)生有責(zé)任道路交通事故 | 下浮30% |
| 上一個(gè)年度發(fā)生一次有責(zé)任不涉及死亡的道路交通事故 | 0% |
| 上一個(gè)年度發(fā)生兩次及兩次以上有責(zé)任道路交通事故 | 上浮10% |
| 上一個(gè)年度發(fā)生有責(zé)任道路交通死亡事故 | 上浮30% |
某機(jī)購(gòu)為了研究某一品牌普通6座以下私家車(chē)的投保情況,隨機(jī)抽取了60輛車(chē)齡已滿三年的該品牌同型號(hào)私家車(chē)的下一年續(xù)保時(shí)的情況,統(tǒng)計(jì)得到了下面的表格:
類(lèi)型 |
|
|
|
|
|
|
數(shù)量 | 10 | 5 | 5 | 20 | 15 | 5 |
(1)求一輛普通6座以下私家車(chē)在第四年續(xù)保時(shí)保費(fèi)高于基本保費(fèi)的頻率;
(2)某二手車(chē)銷(xiāo)售商專(zhuān)門(mén)銷(xiāo)售這一品牌的二手車(chē),且將下一年的交強(qiáng)險(xiǎn)保費(fèi)高于基本保費(fèi)的車(chē)輛記為事故車(chē),假設(shè)購(gòu)進(jìn)一輛事故車(chē)虧損5000元,一輛非事用戶車(chē)盈利10000元,且各種投保類(lèi)型車(chē)的頻率與上述機(jī)構(gòu)調(diào)查的頻率一致,完成下列問(wèn)題:
①若該銷(xiāo)售商店內(nèi)有六輛(車(chē)齡已滿三年)該品牌二手車(chē),某顧客欲在店內(nèi)隨機(jī)挑選兩輛車(chē),求這兩輛車(chē)恰好有一輛為事故車(chē)的概率;
②若該銷(xiāo)售商一次購(gòu)進(jìn)120輛(車(chē)齡已滿三年)該品牌二手車(chē),求一輛車(chē)盈利的平均值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com