
(1) (2)
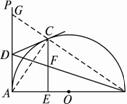
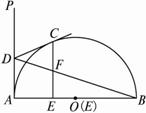
圖13
(1)當點C為![]() 的中點時(如圖13(1)),求證:CF =EF;
的中點時(如圖13(1)),求證:CF =EF;
(2)當點C不是![]() 的中點時(如圖13(2)),試判斷CF與EF的相等關系是否保持不變,并證明你的結論.
的中點時(如圖13(2)),試判斷CF與EF的相等關系是否保持不變,并證明你的結論.
思路分析:第(1)題E與O重合,只需證明四邊形DAEC為矩形,CD∥AB即可.?
(2)由(1)的結論猜測CF =EF仍然成立.然后再設法證明.
證明:(1)∵DA是切線,AB為直徑,∴DA⊥AB.?
∵點C是![]() 的中點,且CE⊥AB,?
的中點,且CE⊥AB,?
∴CE過圓心.∴點E為半圓的圓心.?
又∵DC是切線,∴DC⊥EC.?
∴四邊形DAEC為矩形.?
∴CE∥AD且CE =AD.?
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() ,?
,?
∴F為EC的中點,即CF =EF.?

(2)CF =EF仍然成立.證明如下:?
連結BC并延長交AP于G點,連結AC.?
∵AD、CD是半圓的切線,?
∴DC=DA.∴∠DAC=∠DCA.?
∵AB為直徑,?
∴∠ACB =90°,∠ACG =90°,∠G+∠DAC =∠DCA +∠DCG =90°.?
∴∠G = ∠DCG.?
在△GDC中,GD =DC,又∵DC =DA,∴GD =DA.?
∵AP是半圓O的切線,?
∴AP⊥AB.又CE⊥AB,∴CE∥AP.?
∴![]() =
=![]() =
=![]() .?
.?
又GD =AD,∴CF =EF.


 優百分課時互動系列答案
優百分課時互動系列答案 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案科目:高中數學 來源: 題型:
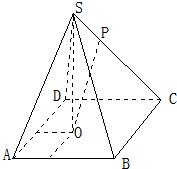 如圖,已知四棱錐S-ABCD的底面是邊長為4的正方形,S在底面上的射影O落在正方形ABCD內,且O到AB、AD的距離分別為2和1. P是SC上的點,
如圖,已知四棱錐S-ABCD的底面是邊長為4的正方形,S在底面上的射影O落在正方形ABCD內,且O到AB、AD的距離分別為2和1. P是SC上的點,| SP |
| PC |
| 1 |
| 3 |
| AB |
| SC |
查看答案和解析>>
科目:高中數學 來源: 題型:
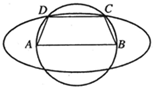 如圖,已知AB=2c(常數c>0),以AB為直徑的圓有一內接梯形ABCD,且AB∥CD,若橢圓以A,B為焦點,且過C,D兩點,則當梯形ABCD的周長最大時,橢圓的離心率為
如圖,已知AB=2c(常數c>0),以AB為直徑的圓有一內接梯形ABCD,且AB∥CD,若橢圓以A,B為焦點,且過C,D兩點,則當梯形ABCD的周長最大時,橢圓的離心率為| 3 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2011•孝感模擬)如圖,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,側棱與底面所成的角為θ,且
(2011•孝感模擬)如圖,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,側棱與底面所成的角為θ,且| 1 | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2011•崇明縣二模)如圖,已知橢圓
(2011•崇明縣二模)如圖,已知橢圓| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 3 |
| 3 |
| π |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com