
【題目】已知f(x)=ax2﹣2lnx,x∈(0,e],其中e是自然對數的底.
(1)若f(x)在x=1處取得極值,求a的值;
(2)求f(x)的單調區間.
【答案】
(1)解:∵f(x)=ax2﹣2lnx,x∈(0,e],
∴f′(x)=2ax﹣ ![]() =
= ![]() ,
,
當x=1時,f(x)取到極值,∴f′(1)=0,解得a=1;
當a=1時,f′(x)= ![]() 在(0,1)上小于0,∴f(x)是減函數,
在(0,1)上小于0,∴f(x)是減函數,
f′(x)= ![]() 在(1,e]上大于0,∴f(x)是增函數,
在(1,e]上大于0,∴f(x)是增函數,
∴f(1)是函數的極小值,此時a的值為1;
(2)解:∵f′(x)=2ax﹣ ![]() =
= ![]() ,x∈(0,e],
,x∈(0,e],
當a≤0時,f′(x)<0恒成立,∴f(x)在(0,e]上是減函數,∴(0,e]是單調減區間;
當a>0時,令f′(x)=0,則 ![]() =0,∴ax2﹣1=0,解得x=
=0,∴ax2﹣1=0,解得x= ![]() ,
,
①若a> ![]() ,則f′(x)在(0,
,則f′(x)在(0, ![]() )上小于0,f(x)是減函數,∴(0,
)上小于0,f(x)是減函數,∴(0, ![]() )是單調減區間;
)是單調減區間;
f′(x)在( ![]() ,e]上大于0,f(x)是增函數,∴(
,e]上大于0,f(x)是增函數,∴( ![]() ,e]是單調增區間;
,e]是單調增區間;
②若a≤ ![]() ,則f′(x)在(0,e]上小于0,f(x)是減函數,∴(0,e]是單調減區間;
,則f′(x)在(0,e]上小于0,f(x)是減函數,∴(0,e]是單調減區間;
綜上,當a≤ ![]() 時,(0,e]是f(x)的單調減區間;
時,(0,e]是f(x)的單調減區間;
當a> ![]() 時,(0,
時,(0, ![]() )是f(x)的單調減區間,(
)是f(x)的單調減區間,( ![]() ,e]是f(x)的單調增區間.
,e]是f(x)的單調增區間.
【解析】(1)當x=1時,f(x)取到極值,即f′(1)=0,從而求得a的值;(2)求出f′(x),其中x∈(0,e],討論f′(x)在a>0、a≤0時,是否大于0?小于0?從而確定f(x)的單調區間.
【考點精析】關于本題考查的利用導數研究函數的單調性和函數的極值與導數,需要了解一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值才能得出正確答案.
是極小值才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】設A(n)表示正整數n的個位數,an=A(n2)﹣A(n),A為數列{an}的前202項和,函數f(x)=ex﹣e+1,若函數g(x)滿足f[g(x)﹣ ![]() ]=1,且bn=g(n)(n∈N*),則數列{bn}的前n項和為 .
]=1,且bn=g(n)(n∈N*),則數列{bn}的前n項和為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,PA⊥☉O所在的平面,AB是☉O的直徑,C是☉O上的一點,AE⊥PB于E,AF⊥PC于F,給出下列結論:①BC⊥平面PAC;②AF⊥平面PCB;③EF⊥PB;④AE⊥平面PBC.其中正確命題的個數是( )
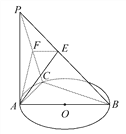
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】AB是☉O的直徑,點C是☉O上的動點(點C不與A,B重合),過動點C的直線VC垂直于☉O所在的平面,D,E分別是VA,VC的中點,則下列結論中正確的是________(填寫正確結論的序號).
(1)直線DE∥平面ABC.
(2)直線DE⊥平面VBC.
(3)DE⊥VB.
(4)DE⊥AB.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體ABCD-A′B′C′D′的棱長為a,連接A′C′,A′D,A′B,BD,BC′,C′D,得到一個三棱錐.求:
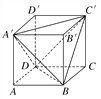
(1)三棱錐A′-BC′D的表面積與正方體表面積的比值;
(2)三棱錐A′-BC′D的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在R上的函數f(x)滿足f(x﹣1)的對稱軸為x=1,f(x+1)= ![]() (f(x)≠0),且在區間(1,2)上單調遞減,已知α、β是鈍角三角形中兩銳角,則f(sinα)和f(cosβ)的大小關系是( )
(f(x)≠0),且在區間(1,2)上單調遞減,已知α、β是鈍角三角形中兩銳角,則f(sinα)和f(cosβ)的大小關系是( )
A.f(sinα)>f(cosβ)
B.f(sinα)<f(cosβ)
C.f(sinα)=f(cosβ)
D.以上情況均有可能
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖是甲、乙兩人在一次射擊比賽中中靶的情況(擊中靶中心的圓面為10環,靶中各數字表示該數字所在圓環被擊中所得的環數),每人射擊了6次.
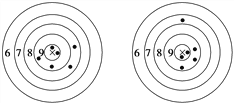
甲射擊的靶 乙射擊的靶
(1)請用列表法將甲、乙兩人的射擊成績統計出來;
(2)請你用學過的統計知識,對甲、乙兩人這次的射擊情況進行比較.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=xex , 則( )
A.x=1為f(x)的極大值點
B.x=1為f(x)的極小值點
C.x=﹣1為f(x)的極大值點
D.x=﹣1為f(x)的極小值點
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com