【題目】在直線
上取一點,過
作以
為焦點的橢圓，則當
最小時，橢圓的標準方程為____________________.
【答案】
【解析】
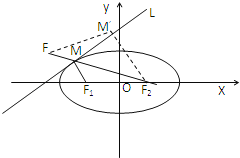
因為|MF1|+|MF2|=2a，即問題轉(zhuǎn)化為在直線上求一點M，使M到F1，F(xiàn)2的距離的和最小，求出F1關(guān)于l的對稱點F，即求M到F、F2的和最小，F(xiàn)F2的長就是所求的最小值．
設(shè)F1（﹣3，0）關(guān)于l：x﹣y+9=0的對稱點 F（x，y）
則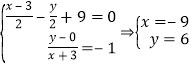
，即F（﹣9，6），
連F2F交l于M，點M即為所求．
F2F：
即x+2y﹣3=0
解方程組
，即M（﹣5，4）
當點M′取異于M的點時，|FM′|+|M′F2|＞|FF2|．
滿足題意的橢圓的長軸
所以
，b2=a2﹣c2=45﹣9=36
所以橢圓的方程為：．
故答案為：
同步學(xué)典一課多練系列答案
經(jīng)典密卷系列答案
金牌課堂練系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)函數(shù)f（x）= 
，若互不相等的實數(shù)x1 ， x2 ， x3滿足f（x1）=f（x2）=f（x3），則x1+x2+x3的取值范圍是（ ）
A.（ 
]
B.（ 
）
C.（ ]
D.（ ）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)f（x）在R上的導(dǎo)函數(shù)為f′（x），若f（x）＜2f′（x）恒成立，且f（ln4）=2，則不等式f（x）＞e 
的解集是（ ）
A.（ln2，+∞）
B.（2ln2，+∞）
C.（﹣∞，ln2）
D.（﹣∞，2ln2）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標系xOy中，已知圓x2+y2﹣12x+32=0的圓心為Q，過點P（0，2）且斜率為k的直線與圓Q相交于不同的兩點A，B．
（1）求k的取值范圍；
（2）是否存在常數(shù)k，使得向量 
與 
共線？如果存在，求k值；如果不存在，請說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)f（x）=2cos（ωx﹣φ）（ω＞0，φ∈[0，π]）的部分圖象如圖所示，若A（ 
， 
），B（ 
， ）．則下列說法錯誤的是（ ） 
A.φ= 
B.函數(shù)f（x）的一條對稱軸為x= 
C.為了得到函數(shù)y=f（x）的圖象，只需將函數(shù)y=2sin2x的圖象向右平移 
個單位
D.函數(shù)f（x）的一個單調(diào)減區(qū)間為[ 
， 
]
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知圓C：x2＋y2＝9，點A(－5，0)，直線l：x－2y＝0.
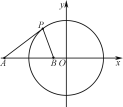
(1)求與圓C相切，且與直線l垂直的直線方程；
(2)在直線OA上(O為坐標原點)，存在定點B(不同于點A)，滿足：對于圓C上任一點P，都有
為一常數(shù)，試求所有滿足條件的點B的坐標．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)函數(shù)f（x）= 
（x＞0），觀察：
f1（x）=f（x）= ，
f2（x）=f（f1（x））= 
；
f3（x）=f（f2（x））= 
．
f4（x）=f（f3（x））= 
…
根據(jù)以上事實，當n∈N*時，由歸納推理可得：fn（1）= ．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
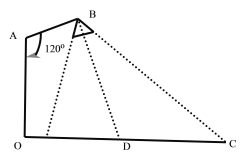
【題目】在路邊安裝路燈,燈柱
的高為
米，路寬
為23米，燈桿
與燈柱
角，路燈采用錐形燈罩，燈罩軸線
與燈桿垂直，請你建立適當直角坐標系，解決以下問題:
(1)當
（2）
且燈罩軸線正好通過道路路面的中線時，求燈桿的長為多少米？
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
