
【題目】已知函數f(x)=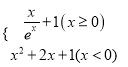 ,若函數y=f(f(x)﹣a)﹣1有三個零點,則a的取值范圍是_____.
,若函數y=f(f(x)﹣a)﹣1有三個零點,則a的取值范圍是_____.
【答案】![]()
【解析】當x<0時,由f(x)﹣1=0得x2+2x+1=1,得x=﹣2或x=0,
當x≥0時,由f(x)﹣1=0得![]() ,得x=0,
,得x=0,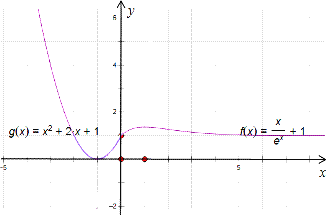
由,y=f(f(x)﹣a)﹣1=0得f(x)﹣a=0或f(x)﹣a=﹣2,
即f(x)=a,f(x)=a﹣2,
作出函數f(x)的圖象如圖:
y=![]() ≥1(x≥0),
≥1(x≥0),
y′=![]() ,當x∈(0,1)時,y′>0,函數是增函數,x∈(1,+∞)時,y′<0,函數是減函數,
,當x∈(0,1)時,y′>0,函數是增函數,x∈(1,+∞)時,y′<0,函數是減函數,
x=1時,函數取得最大值: ![]() ,
,
當1<a﹣2![]() 時,即a∈(3,3+
時,即a∈(3,3+![]() )時,y=f(f(x)﹣a)﹣1有4個零點,
)時,y=f(f(x)﹣a)﹣1有4個零點,
當a﹣2=1+![]() 時,即a=3+
時,即a=3+![]() 時則y=f(f(x)﹣a)﹣1有三個零點,
時則y=f(f(x)﹣a)﹣1有三個零點,
當a>3+![]() 時,y=f(f(x)﹣a)﹣1有1個零點
時,y=f(f(x)﹣a)﹣1有1個零點
當a=1+![]() 時,則y=f(f(x)﹣a)﹣1有三個零點,
時,則y=f(f(x)﹣a)﹣1有三個零點,
當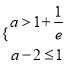 時,即a∈(1+
時,即a∈(1+![]() ,3)時,y=f(f(x)﹣a)﹣1有三個零點.
,3)時,y=f(f(x)﹣a)﹣1有三個零點.
綜上a∈![]() ,函數有3個零點.
,函數有3個零點.
故答案為: ![]() .
.


科目:高中數學 來源: 題型:
【題目】某學校為擔任班主任的教師辦理手機語音月卡套餐,為了解通話時長,采用隨機抽樣的方法,得到該校100位班主任每人的月平均通話時長![]() (單位:分鐘)的數據,其頻率分布直方圖如圖所示,將頻率視為概率.
(單位:分鐘)的數據,其頻率分布直方圖如圖所示,將頻率視為概率.
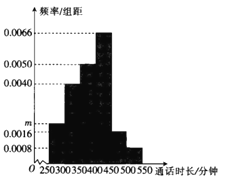
(1)求圖中![]() 的值;
的值;
(2)估計該校擔任班主任的教師月平均通話時長的中位數;
(3)在![]() ,
,![]() 這兩組中采用分層抽樣的方法抽取6人,再從這6人中隨機抽取2人,求抽取的2人恰在同一組的概率.
這兩組中采用分層抽樣的方法抽取6人,再從這6人中隨機抽取2人,求抽取的2人恰在同一組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓的中心在原點,其左焦點![]() 與拋物線
與拋物線![]() 的焦點重合,過
的焦點重合,過![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 、
、![]() 兩點,與拋物線交于
兩點,與拋物線交于![]() 、
、![]() 兩點.當直線
兩點.當直線![]() 與
與![]() 軸垂直時,
軸垂直時,![]() .
.
(1)求橢圓的方程;
(2)求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設![]() 是橢圓
是橢圓![]() 的左焦點,直線:
的左焦點,直線:![]() 與
與![]() 軸交于
軸交于![]() 點,
點,![]() 為橢圓的長軸,已知
為橢圓的長軸,已知![]() ,且
,且![]() ,過
,過![]() 點作斜率為
點作斜率為![]() 直線
直線![]() 與橢圓相交于不同的兩點
與橢圓相交于不同的兩點![]() ,
,
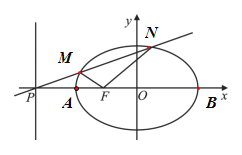
(1)當![]() 時,線段
時,線段![]() 的中點為
的中點為![]() ,過
,過![]() 作
作![]() 交
交![]() 軸于點
軸于點![]() ,求
,求![]() ;
;
(2)求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設復數β=x+yi(x,y∈R)與復平面上點P(x,y)對應.
(1)若β是關于t的一元二次方程t2﹣2t+m=0(m∈R)的一個虛根,且|β|=2,求實數m的值;
(2)設復數β滿足條件|β+3|+(﹣1)n|β﹣3|=3a+(﹣1)na(其中n∈N*、常數![]() ),當n為奇數時,動點P(x、y)的軌跡為C1.當n為偶數時,動點P(x、y)的軌跡為C2.且兩條曲線都經過點
),當n為奇數時,動點P(x、y)的軌跡為C1.當n為偶數時,動點P(x、y)的軌跡為C2.且兩條曲線都經過點![]() ,求軌跡C1與C2的方程;
,求軌跡C1與C2的方程;
(3)在(2)的條件下,軌跡C2上存在點A,使點A與點B(x0,0)(x0>0)的最小距離不小于![]() ,求實數x0的取值范圍.
,求實數x0的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,曲線![]() (
(![]() 為參數),在以原點
為參數),在以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線![]() .
.
(1)寫出![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 在曲線
在曲線![]() 上,點
上,點![]() 在曲線
在曲線![]() 上,求
上,求![]() 的最小值及此時點
的最小值及此時點![]() 的直角坐標.
的直角坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]()
![]() )在
)在![]() 上至少存在兩個不同的
上至少存在兩個不同的![]() ,
,![]() 滿足
滿足![]() ,且
,且![]() 在
在![]() 上具有單調性,點
上具有單調性,點![]() 和直線
和直線![]() 分別為
分別為![]() 圖象的一個對稱中心和一條對稱軸,則下列命題中正確的是( )
圖象的一個對稱中心和一條對稱軸,則下列命題中正確的是( )
A.![]() 的最小正周期為
的最小正周期為![]()
B.![]()
C.![]() 在
在![]() 上是減函數
上是減函數
D.將![]() 圖象上每一點的橫坐標伸長為原來的2倍(縱坐標不變),得到
圖象上每一點的橫坐標伸長為原來的2倍(縱坐標不變),得到![]() 的圖象,則
的圖象,則![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com