
【題目】如圖,在四棱錐P﹣ABCD中,側面PAB⊥底面ABCD,且∠PAB=∠ABC=90°,AD∥BC,PA=AB=BC=2AD,E是PC的中點.
(Ⅰ)求證:DE⊥平面PBC;
(Ⅱ)求二面角A﹣PD﹣E的余弦值.
【答案】(Ⅰ)證明:∵側面PAB⊥底面ABCD,且∠PAB=∠ABC=90°,AD∥BC,
∴PA⊥AB,PA⊥AD⊥AD⊥AB,
以點A為坐標原點,建立如圖所示的坐標系,設PA=AB=BC=2AD=2,則P(0,0,2),D(1,0,0),B(0,2,0),C(2,2,0),E(1,1,1),
∴ ![]() =(0,1,1),
=(0,1,1), ![]() =(0,2,﹣2),
=(0,2,﹣2), ![]() =(2,2,﹣2),
=(2,2,﹣2),
∴ ![]() =0,
=0, ![]() =0,
=0,
∴DE⊥PB,DE⊥PC,
∵PB∩PC=P,
∴DE⊥平面PBC;
(Ⅱ)解:由(Ⅰ)可知平面PAD的一個法向量 ![]() =(0,2,0).
=(0,2,0).
設平面PCD的一個法向量為 ![]() =(x,y,z),則
=(x,y,z),則
∵ ![]() =(1,0,﹣2),
=(1,0,﹣2), ![]() =(2,2,﹣2),
=(2,2,﹣2),
∴ ![]() ,
,
∴取 ![]() =(2,﹣1,1),
=(2,﹣1,1),
∴cos< ![]() ,
, ![]() >=
>= ![]() =﹣
=﹣ ![]() .
.
【解析】(Ⅰ)以點A為坐標原點,建立坐標系,證明 ![]() =0,
=0, ![]() =0,即可證明DE⊥平面PBC;(Ⅱ)求出平面PAD的一個法向量、平面PCD的一個法向量,利用向量的夾角公式,即可求二面角A﹣PD﹣E的余弦值.
=0,即可證明DE⊥平面PBC;(Ⅱ)求出平面PAD的一個法向量、平面PCD的一個法向量,利用向量的夾角公式,即可求二面角A﹣PD﹣E的余弦值.
【考點精析】根據題目的已知條件,利用直線與平面垂直的判定的相關知識可以得到問題的答案,需要掌握一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直;注意點:a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】將函數f(x)=2sin(2x﹣![]() )的圖象向左平移
)的圖象向左平移![]() 個單位,再向上平移1個單位,得到函數y=g(x)的圖象,若y=g(x)在[0,b](b>0)上至少含有10個零點,則b的最小值為
個單位,再向上平移1個單位,得到函數y=g(x)的圖象,若y=g(x)在[0,b](b>0)上至少含有10個零點,則b的最小值為
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高二數學期中測試中,為了了解學生的考試情況,從中抽取了![]() 個學生的成績(滿分為100分)進行統計.按照[50,60), [60,70), [70,80), [80,90), [90,100]的分組作出頻率分布直方圖,并作出樣本分數的莖葉圖(圖中僅列出得分在[50,60), [90,100]的數據).
個學生的成績(滿分為100分)進行統計.按照[50,60), [60,70), [70,80), [80,90), [90,100]的分組作出頻率分布直方圖,并作出樣本分數的莖葉圖(圖中僅列出得分在[50,60), [90,100]的數據).

(1)求樣本容量![]() 和頻率分布直方圖中
和頻率分布直方圖中![]() 的值;
的值;
(2)在選取的樣本中,從成績是80分以上(含80分)的同學中隨機抽取3名參加志愿者活動,所抽取的3名同學中至少有一名成績在[90,100]內的概率。.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某農科所對冬季晝夜溫差大小與某反季節大豆新品種發芽多少之間的關系進行分析研究,他們分別記錄了![]() 月
月![]() 日至
日至![]() 月
月![]() 日的每天晝夜溫差與實驗室每天每
日的每天晝夜溫差與實驗室每天每![]() 顆種子中的發芽數,得到如下資料:
顆種子中的發芽數,得到如下資料:
日期 |
|
|
|
|
|
溫差 |
|
|
|
|
|
發芽數 |
|
|
|
|
|
該農科所確定的研究方案是:先從這![]() 組數據中選取
組數據中選取![]() 組,用剩下的
組,用剩下的![]() 組數據求線性回歸方程,再對被選取的
組數據求線性回歸方程,再對被選取的![]() 組數據進行檢驗.
組數據進行檢驗.
(1)求選取的![]() 組數據恰好是不相鄰兩天數據的概率;
組數據恰好是不相鄰兩天數據的概率;
(2)若選取的是![]() 月
月![]() 日與
日與![]() 月
月![]() 日的數據,請根據
日的數據,請根據![]() 月
月![]() 日至
日至![]() 月
月![]() 日的數據求出
日的數據求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過![]() 顆.則認為得到的線性回歸方程是可靠的.試問(2)中所得到的線性回歸方程是可靠的嗎?
顆.則認為得到的線性回歸方程是可靠的.試問(2)中所得到的線性回歸方程是可靠的嗎?
附:回歸直線的斜率和截距的最小二乘估計公式分別為:
 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某儀器經過檢驗合格才能出廠,初檢合格率為![]() :若初檢不合格,則需要進行調試,經調試后再次對其進行檢驗;若仍不合格,作為廢品處理,再檢合格率為
:若初檢不合格,則需要進行調試,經調試后再次對其進行檢驗;若仍不合格,作為廢品處理,再檢合格率為![]() .每臺儀器各項費用如表:
.每臺儀器各項費用如表:
項目 | 生產成本 | 檢驗費/次 | 調試費 | 出廠價 |
金額(元) | 1000 | 100 | 200 | 3000 |
(Ⅰ)求每臺儀器能出廠的概率;
(Ⅱ)求生產一臺儀器所獲得的利潤為1600元的概率(注:利潤![]() 出廠價
出廠價![]() 生產成本
生產成本![]() 檢驗費
檢驗費![]() 調試費);
調試費);
(Ⅲ)假設每臺儀器是否合格相互獨立,記![]() 為生產兩臺儀器所獲得的利潤,求
為生產兩臺儀器所獲得的利潤,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分) 某居民小區有兩個相互獨立的安全防范系統(簡稱系統)![]() 和
和![]() ,系統
,系統![]() 和
和![]() 在任意時刻發生故障的概率分別為
在任意時刻發生故障的概率分別為![]() 和
和![]() 。
。
(Ⅰ)若在任意時刻至少有一個系統不發生故障的概率為![]() ,求
,求![]() 的值;
的值;
(Ⅱ)設系統![]() 在3次相互獨立的檢測中不發生故障的次數為隨機變量
在3次相互獨立的檢測中不發生故障的次數為隨機變量![]() ,求
,求![]() 的概率分布列及數學期望
的概率分布列及數學期望![]() 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() 的右頂點A(2,0),且過點
的右頂點A(2,0),且過點 ![]()
(Ⅰ)求橢圓C的方程;
(Ⅱ)過點B(1,0)且斜率為k1(k1≠0)的直線l于橢圓C相交于E,F兩點,直線AE,AF分別交直線x=3于M,N兩點,線段MN的中點為P,記直線PB的斜率為k2 , 求證:k1k2為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國北斗衛星導航系統是中國自行研制的全球衛星導航系統,作為國家戰略性空間基礎設施,我國北斗衛星導航系統不僅對國防安全意義重大,而且在民用領域的精準化應用也越來越廣泛.據統計,2016年衛星導航與位置服務產業總產值達到2118億元,較2015年約增長![]() .下面是40個城市北斗衛星導航系統與位置服務產業的產值(單位:萬元)的頻率分布直方圖:
.下面是40個城市北斗衛星導航系統與位置服務產業的產值(單位:萬元)的頻率分布直方圖:
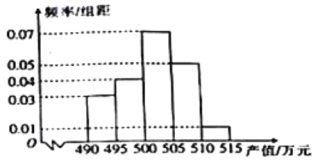
(1)根據頻率分布直方圖,求產值小于500萬元的城市個數;
(2)在上述抽取的40個城市中任取2個,設![]() 為產值不超過500萬元的城市個數,求
為產值不超過500萬元的城市個數,求![]() 的分布列及期望和方差.
的分布列及期望和方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現在很多人喜歡自助游,2017年孝感楊店桃花節,美麗的桃花風景和人文景觀迎來眾多賓客.某調查機構為了了解“自助游”是否與性別有關,在孝感桃花節期間,隨機抽取了![]() 人,得如下所示的列聯表:
人,得如下所示的列聯表:
贊成“自助游” | 不贊成“自助游” | 合計 | |
男性 |
| ||
女性 |
| ||
合計 |
|
(1)若在![]() 這人中,按性別分層抽取一個容量為
這人中,按性別分層抽取一個容量為![]() 的樣本,女性應抽
的樣本,女性應抽![]() 人,請將上面的列聯表補充完整,并據此資料能否在犯錯誤的概率不超過
人,請將上面的列聯表補充完整,并據此資料能否在犯錯誤的概率不超過![]() 前提下,認為贊成“自助游”是與性別有關系?
前提下,認為贊成“自助游”是與性別有關系?
(2)若以抽取樣本的頻率為概率,從旅游節大量游客中隨機抽取![]() 人贈送精美紀念品,記這
人贈送精美紀念品,記這![]() 人中贊成“自助游”人數為
人中贊成“自助游”人數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
附: 
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com