
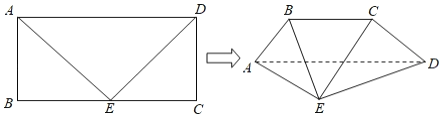
【題目】如圖,矩形![]() 中,
中,![]() ,
,![]() 為
為![]() 的中點(diǎn),現(xiàn)將
的中點(diǎn),現(xiàn)將![]() 與
與![]() 折起,使得平面
折起,使得平面![]() 及平面
及平面![]() 都與平面
都與平面![]() 垂直.
垂直.
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
【答案】(1)見(jiàn)解析(2)![]()
【解析】
(1)分別取![]() 的中點(diǎn)
的中點(diǎn)![]() ,由線(xiàn)面垂直性質(zhì)定理可得
,由線(xiàn)面垂直性質(zhì)定理可得![]() ,又三角形
,又三角形![]() 和
和![]() 全等,所以
全等,所以![]() ,四邊形
,四邊形![]() 為平行四邊形,根據(jù)線(xiàn)面平行的判定定理,即得證;
為平行四邊形,根據(jù)線(xiàn)面平行的判定定理,即得證;
(2)以![]() 為原點(diǎn),
為原點(diǎn),![]() ,
,![]() 為
為![]() ,
,![]() 正半軸,過(guò)
正半軸,過(guò)![]() 作平面
作平面![]() 的垂線(xiàn)為
的垂線(xiàn)為![]() 軸,建立空間直角坐標(biāo)系,利用向量法即可求出二面角
軸,建立空間直角坐標(biāo)系,利用向量法即可求出二面角![]() 的正弦值.
的正弦值.
(1)如圖所示: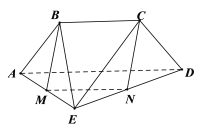
分別取![]() ,
,![]() 的中點(diǎn)
的中點(diǎn)![]() ,
,![]() ,連結(jié)
,連結(jié)![]() ,
,![]() ,
,![]() ,
,
則![]() ,
,![]() ,
,
![]() 平面
平面![]() 與平面
與平面![]() 都與平面
都與平面![]() 垂直,
垂直,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
由線(xiàn)面垂直的性質(zhì)定理得![]() ,
,
![]() ,四邊形
,四邊形![]() 是平行四邊形,
是平行四邊形,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
(2)如圖,以![]() 為原點(diǎn),
為原點(diǎn),![]() ,
,![]() 為
為![]() ,
,![]() 正半軸,過(guò)
正半軸,過(guò)![]() 作平面
作平面![]() 的垂線(xiàn)為
的垂線(xiàn)為![]() 軸,建立空間直角坐標(biāo)系,則
軸,建立空間直角坐標(biāo)系,則![]() ,
,![]() ,平面
,平面![]() 的法向量
的法向量![]() ,
,
設(shè)平面![]() 的法向量
的法向量![]() ,
,
則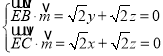 ,取
,取![]() ,得
,得![]() .
.
設(shè)二面角![]() 的平面角為
的平面角為![]() ,由圖知
,由圖知![]() 為鈍角,
為鈍角,
![]() .
.
∴二面角![]() 的余弦值為
的余弦值為![]() ,則正弦值為
,則正弦值為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知圓![]() ,直線(xiàn)
,直線(xiàn)![]() 的方程為
的方程為![]() ,點(diǎn)
,點(diǎn)![]() 是直線(xiàn)
是直線(xiàn)![]() 上一動(dòng)點(diǎn),過(guò)點(diǎn)
上一動(dòng)點(diǎn),過(guò)點(diǎn)![]() 作圓的切線(xiàn)
作圓的切線(xiàn)![]() 、
、![]() ,切點(diǎn)為
,切點(diǎn)為![]() 、
、![]() .
.
(1)當(dāng)![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() 時(shí),求
時(shí),求![]() 的大小;
的大小;
(2)求四邊形![]() 面積的最小值;
面積的最小值;
(3)求證:經(jīng)過(guò)![]() 、
、![]() 、
、![]() 三點(diǎn)的圓
三點(diǎn)的圓![]() 必過(guò)定點(diǎn),并求出所有定點(diǎn)的坐標(biāo).
必過(guò)定點(diǎn),并求出所有定點(diǎn)的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列說(shuō)法中正確的序號(hào)是____________(寫(xiě)出所有正確命題的序號(hào))
(1)“![]() 為實(shí)數(shù)”是“
為實(shí)數(shù)”是“![]() 為有理數(shù)”的充分不必要條件;
為有理數(shù)”的充分不必要條件;
(2)“![]() ”是“
”是“![]() ”的充要條件
”的充要條件
(3)“![]() ”是“
”是“![]() ”的必要不充分條件;
”的必要不充分條件;
(4)“![]() ,
,![]() ”是“
”是“![]() ”的充分不必要條件;
”的充分不必要條件;
(5)![]() 的三個(gè)內(nèi)角為
的三個(gè)內(nèi)角為![]() .“
.“![]() ”是“
”是“![]() ”的充要條件
”的充要條件
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 經(jīng)過(guò)點(diǎn)
經(jīng)過(guò)點(diǎn)![]() ,且離心率為
,且離心率為![]() .
.
(1)設(shè)過(guò)點(diǎn)![]() 的直線(xiàn)與橢圓
的直線(xiàn)與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點(diǎn),若
兩點(diǎn),若![]() 的中點(diǎn)恰好為點(diǎn)
的中點(diǎn)恰好為點(diǎn)![]() ,求該直線(xiàn)的方程;
,求該直線(xiàn)的方程;
(2)過(guò)右焦點(diǎn)![]() 的直線(xiàn)
的直線(xiàn)![]() (與
(與![]() 軸不重合)與橢圓
軸不重合)與橢圓![]() 交于
交于![]() 兩點(diǎn),線(xiàn)段
兩點(diǎn),線(xiàn)段![]() 的垂直平分線(xiàn)交
的垂直平分線(xiàn)交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為評(píng)估設(shè)備![]() 生產(chǎn)某種零件的性能,從設(shè)備
生產(chǎn)某種零件的性能,從設(shè)備![]() 生產(chǎn)該零件的流水線(xiàn)上隨機(jī)抽取100個(gè)零件為樣本,測(cè)量其直徑后,整理得到下表:
生產(chǎn)該零件的流水線(xiàn)上隨機(jī)抽取100個(gè)零件為樣本,測(cè)量其直徑后,整理得到下表:
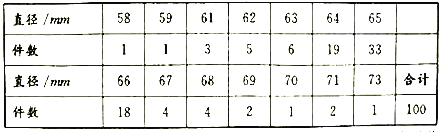
經(jīng)計(jì)算,樣本的平均值![]() ,標(biāo)準(zhǔn)差
,標(biāo)準(zhǔn)差![]() ,以頻率值作為概率的估計(jì)值.
,以頻率值作為概率的估計(jì)值.
(I)為評(píng)判一臺(tái)設(shè)備的性能,從該設(shè)備加工的零件中任意抽取一件,記其直徑為![]() ,并根據(jù)以下不等式進(jìn)行判定(
,并根據(jù)以下不等式進(jìn)行判定(![]() 表示相應(yīng)事件的概率):
表示相應(yīng)事件的概率):
①![]() ;
;
②![]() ;
;
③![]() .
.
判定規(guī)則為:若同時(shí)滿(mǎn)足上述三個(gè)式子,則設(shè)備等級(jí)為甲;若僅滿(mǎn)足其中兩個(gè),則等級(jí)為乙,若僅滿(mǎn)足其中一個(gè),則等級(jí)為丙;若全部都不滿(mǎn)足,則等級(jí)為了.試判斷設(shè)備![]() 的性能等級(jí).
的性能等級(jí).
(Ⅱ)將直徑尺寸在![]() 之外的零件認(rèn)定為是“次品”.
之外的零件認(rèn)定為是“次品”.
①?gòu)脑O(shè)備![]() 的生產(chǎn)流水線(xiàn)上隨機(jī)抽取2個(gè)零件,求其中次品個(gè)數(shù)
的生產(chǎn)流水線(xiàn)上隨機(jī)抽取2個(gè)零件,求其中次品個(gè)數(shù)![]() 的數(shù)學(xué)期望
的數(shù)學(xué)期望![]() ;
;
②從樣本中隨意抽取2個(gè)零件,求其中次品個(gè)數(shù)![]() 的數(shù)學(xué)期望
的數(shù)學(xué)期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在平面直角坐標(biāo)系![]() 中,直線(xiàn)
中,直線(xiàn)![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)),在以坐標(biāo)原點(diǎn)為極點(diǎn),
為參數(shù)),在以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸的正半軸為極軸的極坐標(biāo)系中,曲線(xiàn)
軸的正半軸為極軸的極坐標(biāo)系中,曲線(xiàn)![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() (
(![]() 且
且![]() ).
).
(I)求直線(xiàn)![]() 的極坐標(biāo)方程及曲線(xiàn)
的極坐標(biāo)方程及曲線(xiàn)![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(Ⅱ)已知![]() 是直線(xiàn)
是直線(xiàn)![]() 上的一點(diǎn),
上的一點(diǎn),![]() 是曲線(xiàn)
是曲線(xiàn)![]() 上的一點(diǎn),
上的一點(diǎn), ![]() ,
,![]() ,若
,若![]() 的最大值為2,求
的最大值為2,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖的空間幾何體中,四邊形![]() 為邊長(zhǎng)為2的正方形,
為邊長(zhǎng)為2的正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
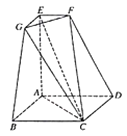
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值.
所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】選修4-5:不等式選講
已知函數(shù)![]() .
.
(1)若![]() ,求不等式
,求不等式![]() 的解集;
的解集;
(2)若![]() 時(shí),
時(shí),![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com