
【題目】某企業一天中不同時刻的用電量![]() (萬千瓦時)關于時間
(萬千瓦時)關于時間![]() (單位:小時,其中
(單位:小時,其中![]() 對應凌晨0點)的函數
對應凌晨0點)的函數![]() 近似滿足
近似滿足![]()
![]() ,如圖是函數
,如圖是函數![]() 的部分圖象.
的部分圖象.

(1)求![]() 的解析式;
的解析式;
(2)已知該企業某天前半日能分配到的供電量![]() (萬千瓦時)與時間
(萬千瓦時)與時間![]() (小時)的關系可用線性函數模型
(小時)的關系可用線性函數模型![]() 模擬,當供電量
模擬,當供電量![]() 小于企業用電量
小于企業用電量![]() 時,企業必須停產.初步預計開始停產的臨界時間
時,企業必須停產.初步預計開始停產的臨界時間![]() 在中午11點到12點之間,用二分法估算
在中午11點到12點之間,用二分法估算![]() 所在的一個區間(區間長度精確到15分鐘).
所在的一個區間(區間長度精確到15分鐘).
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由圖象,利用最大值與最小值差的一半求得![]() ,由最大值與最小值和的一半求得
,由最大值與最小值和的一半求得![]() ,由周期求得
,由周期求得![]() ,由特殊點求得
,由特殊點求得![]() 的值,從而可得
的值,從而可得![]() 的解析式; (2)構造函數
的解析式; (2)構造函數![]() ,先判斷
,先判斷![]() 在
在![]() 上是單調遞增函數,再利用二分法判斷函數
上是單調遞增函數,再利用二分法判斷函數![]() 的零點所在的區間.
的零點所在的區間.
(1)由圖象可知A=![]() =
=![]() ,B=
,B=![]() =2,T=12=
=2,T=12=![]() ,ω=
,ω=![]() ,
,
代入點(0,2.5)得sinφ=1,
∵0<φ<π,∴φ=![]() ;
;
綜上,A=![]() ,B=2,ω=
,B=2,ω=![]() ,φ=
,φ=![]() ,
,
即f(t)=![]() sin(
sin(![]() t+
t+![]() )+2.
)+2.
(2)由(1)知f(t)=![]() sin(
sin(![]() t+
t+![]() )+2=
)+2=![]() cos
cos![]() t+2,
t+2,
令h(t)=f(t)-g(t),
設h(t0)=0,則t0為該企業的開始停產的臨界時間;
易知h(t)在(11,12)上是單調遞增函數;
由h(11)=f(11)-g(11)=![]() cos
cos![]() +2+2×11-25=
+2+2×11-25=![]() -1<0,
-1<0,
h(12)=f(12)-g(12)=![]() cos
cos![]() +2+2×12-25=
+2+2×12-25=![]() >0,
>0,
又h(11.5)=f(11.5)-g(11.5)=![]() cos
cos![]() +2+2×11.5-25=
+2+2×11.5-25=![]() cos(-
cos(-![]() )=
)=![]() cos
cos![]() =
=![]() >0,
>0,
則t0∈(11,11.5),即11點到11點30分之間(大于15分鐘),
又h(11.25)=f(11.25)-g(11.25)=![]() cos
cos![]() +2+2×11.25-25<
+2+2×11.25-25<![]() ×1-0.5=0,
×1-0.5=0,
則t0∈(11.25,11.5),即11點15分到11點30分之間(正好15分鐘).
所以,企業開始停產的臨界時間t0所在的區間為(11.25,11.5).


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】由中央電視臺綜合頻道(![]() )和唯眾傳媒聯合制作的《開講啦》是中國首檔青春電視公開課。每期節目由一位知名人士講述自己的故事,分享他們對于生活和生命的感悟,給予中國青年現實的討論和心靈的滋養,討論青年們的人生問題,同時也在討論青春中國的社會問題,受到青年觀眾的喜愛,為了了解觀眾對節目的喜愛程度,電視臺隨機調查了
)和唯眾傳媒聯合制作的《開講啦》是中國首檔青春電視公開課。每期節目由一位知名人士講述自己的故事,分享他們對于生活和生命的感悟,給予中國青年現實的討論和心靈的滋養,討論青年們的人生問題,同時也在討論青春中國的社會問題,受到青年觀眾的喜愛,為了了解觀眾對節目的喜愛程度,電視臺隨機調查了![]() 、
、![]() 兩個地區的100名觀眾,得到如下的
兩個地區的100名觀眾,得到如下的![]() 列聯表:
列聯表:
非常滿意 | 滿意 | 合計 | |
| 30 |
| |
|
|
| |
合計 |
已知在被調查的100名觀眾中隨機抽取1名,該觀眾是![]() 地區當中“非常滿意”的觀眾的概率為
地區當中“非常滿意”的觀眾的概率為![]() ,且
,且![]() .
.
(Ⅰ)現從100名觀眾中用分層抽樣的方法抽取20名進行問卷調查,則應抽取“滿意”的![]() 、
、![]() 地區的人數各是多少;
地區的人數各是多少;
(Ⅱ)完成上述表格,并根據表格判斷是否有![]() 的把握認為觀眾的滿意程度與所在地區有關系;
的把握認為觀眾的滿意程度與所在地區有關系;
(Ⅲ)若以抽樣調查的頻率為概率,從![]() 地區隨機抽取3人,設抽到的觀眾“非常滿意”的人數為
地區隨機抽取3人,設抽到的觀眾“非常滿意”的人數為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
|
|
|
|
|
|
|
|
|
|
附:參考公式:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了更好地規劃進貨的數量,保證蔬菜的新鮮程度,某蔬菜商店從某一年的銷售數據中,隨機抽取了8組數據作為研究對象,如表所示(![]() (噸)為買進蔬菜的數量,
(噸)為買進蔬菜的數量,![]() (天)為銷售天數):
(天)為銷售天數):
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
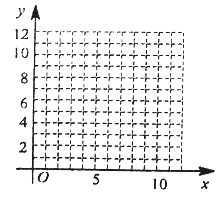
(1)根據上表數據在所給坐標系中繪制散點圖,并用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)根據(Ⅰ)中的計算結果,該蔬菜商店準備一次性買進25噸,預計需要銷售多少天?
(參考數據和公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,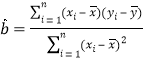
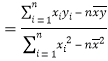 ,
,![]() .)
.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正項數列{an}的前n項和Sn滿足:Sn2 ![]()
(1)求數列{an}的通項公式an;
(2)令b ![]() ,數列{bn}的前n項和為Tn . 證明:對于任意n∈N* , 都有
,數列{bn}的前n項和為Tn . 證明:對于任意n∈N* , 都有 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙、丁四位同學高考之后計劃去![]() 三個不同社區進行幫扶活動,每人只能去一個社區,每個社區至少一人.其中甲必須去
三個不同社區進行幫扶活動,每人只能去一個社區,每個社區至少一人.其中甲必須去![]() 社區,乙不去
社區,乙不去![]() 社區,則不同的安排方法種數為 ( )
社區,則不同的安排方法種數為 ( )
A. 24 B. 8 C. 7 D. 6
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com