
【題目】已知函數(shù)![]() 在
在![]() 處有極值10.
處有極值10.
(1)求實(shí)數(shù)![]() 的值;
的值;
(2)設(shè)![]() ,討論函數(shù)
,討論函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的單調(diào)性.
上的單調(diào)性.
【答案】(1) ![]() ;(2)答案見解析.
;(2)答案見解析.
【解析】試題分析:(1)根據(jù)題意得到關(guān)于m的方程組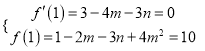 ,解方程組求得
,解方程組求得![]() 即可;(2)先判斷函數(shù)
即可;(2)先判斷函數(shù)![]() 的單調(diào)性,然后根據(jù)
的單調(diào)性,然后根據(jù)![]() 的取值情況分類討論判斷函數(shù)
的取值情況分類討論判斷函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的單調(diào)性。
上的單調(diào)性。
試題解析:
(1)![]() 定義域?yàn)?/span>
定義域?yàn)?/span>![]() ,
,
∵![]() 在
在![]() 處有極值10,
處有極值10,
∴![]() 且
且![]() ,
,
即![]() ,
,
解得: 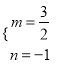 或
或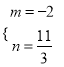 ,
,
當(dāng)![]() 時(shí),
時(shí), ![]() ,
,
當(dāng)![]() 時(shí),
時(shí), ![]() ,
,
∴![]() 在
在![]() 處有極值10時(shí),
處有極值10時(shí), ![]() .
.
(2)由(1)可知![]() ,
,
∴![]()
當(dāng)![]() 變化時(shí),
變化時(shí), ![]() 的變化情況如下表:
的變化情況如下表:
|
|
|
| 1 |
|
| + | 0 | - | 0 | + |
| 增 | 極大 | 減 | 極小 | 增 |
∴①當(dāng)![]() ,即
,即![]() 時(shí),
時(shí), ![]() 在區(qū)間
在區(qū)間![]() 上的單調(diào)遞增;
上的單調(diào)遞增;
②當(dāng)![]() ,即
,即![]() 時(shí),
時(shí), ![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞增,在區(qū)間
上單調(diào)遞增,在區(qū)間![]() 上單調(diào)遞減;
上單調(diào)遞減;
③當(dāng)![]() 且
且![]() ,即
,即![]() 時(shí),
時(shí), ![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減;
上單調(diào)遞減;
④當(dāng)![]() ,即
,即![]() 時(shí),
時(shí), ![]() 在區(qū)間
在區(qū)間![]() 上的單調(diào)遞減,在區(qū)間
上的單調(diào)遞減,在區(qū)間![]() 上單調(diào)遞增;
上單調(diào)遞增;
⑤當(dāng)![]() 時(shí),
時(shí), ![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞增.
上單調(diào)遞增.
綜上所述:
當(dāng)![]() 或
或![]() 時(shí),
時(shí), ![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞增;
上單調(diào)遞增;
當(dāng)![]() 時(shí),
時(shí), ![]() 在區(qū)間上
在區(qū)間上![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減;
上單調(diào)遞減;
當(dāng)![]() 時(shí),
時(shí), ![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減;
上單調(diào)遞減;
當(dāng)![]() 時(shí),
時(shí), ![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增.
上單調(diào)遞增.


 字詞句篇與同步作文達(dá)標(biāo)系列答案
字詞句篇與同步作文達(dá)標(biāo)系列答案 走進(jìn)文言文系列答案
走進(jìn)文言文系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】由大于0的自然數(shù)構(gòu)成的等差數(shù)列{an},它的最大項(xiàng)為26,其所有項(xiàng)的和為70;
(1)求數(shù)列{an}的項(xiàng)數(shù)n;
(2)求此數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在調(diào)查男女乘客是否暈機(jī)的情況中,已知男乘客暈機(jī)為28人,不會(huì)暈機(jī)的也是28人,而女乘客暈機(jī)為28人,不會(huì)暈機(jī)的為56人,![]() 其中
其中 ![]() 為樣本容量。
為樣本容量。
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)根據(jù)以上數(shù)據(jù)建立一個(gè) ![]() 的列聯(lián)表;
的列聯(lián)表;
(2)試判斷是否有95%的把握認(rèn)為是否暈機(jī)與性別有關(guān)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知定義域?yàn)?/span>![]() 的函數(shù)
的函數(shù)![]() 存在兩個(gè)零點(diǎn).
存在兩個(gè)零點(diǎn).
(1)求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(2)若![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知O、A、B三地在同一水平面內(nèi),A地在O地正東方向2km處,B地在O地正北方向2km處,某測繪隊(duì)員在A、B之間的直線公路上任選一點(diǎn)C作為測繪點(diǎn),用測繪儀進(jìn)行測繪,O地為一磁場,距離其不超過![]() km的范圍內(nèi)會(huì)測繪儀等電子儀器形成干擾,使測量結(jié)果不準(zhǔn)確,則該測繪隊(duì)員能夠得到準(zhǔn)確數(shù)據(jù)的概率是( )
km的范圍內(nèi)會(huì)測繪儀等電子儀器形成干擾,使測量結(jié)果不準(zhǔn)確,則該測繪隊(duì)員能夠得到準(zhǔn)確數(shù)據(jù)的概率是( )
A.1-![]()
B.![]()
C.1-![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=log2(x+1),g(x)=log2(3x+1).
(1)求出使g(x)≥f(x)成立的x的取值范圍;
(2)在(1)的范圍內(nèi)求y=g(x)﹣f(x)的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知海島A到海岸公路BC的距離AB=50km,B,C間的距離為100km,從A到C必須先坐船到BC上的某一點(diǎn)D,航速為25km/h,再乘汽車到C,車速為50km/h,記∠BDA=θ
(1)試將由A到C所用的時(shí)間t表示為θ的函數(shù)t(θ);
(2)問θ為多少時(shí),由A到C所用的時(shí)間t最少?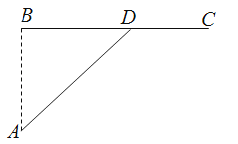
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com