【題目】在銳角△ABC中，a、b、c分別為∠A、∠B、∠C所對的邊，且 
（1）確定∠C的大小；
（2）若c= 
，求△ABC周長的取值范圍．
【答案】
（1）解：由 
a=2csinA，
由正弦定理，得 sinA=2sinCsinA，
又sinA≠0，
則sinC= 
，
∴∠C=60°或∠C=120°，
∵△ABC為銳角三角形，
∴∠C=120°舍去．
∴∠C=60°
（2）解：∵c= ，sinC=
∴由正弦定理得： 
，
即a=2sinA，b=2sinB，
又A+B=π﹣C= 
，即B= ﹣A，
∴a+b+c=2（sinA+sinB）+
=2[sinA+sin（ ﹣A）]+
=2（sinA+sin cosA﹣cos sinA）+
=3sinA+ cosA+
=2 （sinAcos 
+cosAsin ）+
=2 sin（A+ ）+ ，
∵△ABC是銳角三角形，
∴ ＜∠A＜ 
，
∴ ＜sin（A+ ）≤1，
則△ABC周長的取值范圍是（3+ ，3 ]
【解析】（1）由正弦定理進行邊角互化，求出sinC=，由于三角形ABC為銳角三角形，故∠C=60°，（2）根據正弦定理進行邊角互化，得出a=2sinA，b=2sinB，由輔助角公式和兩角差的正弦公式進行化簡，結合正弦公式即可得到△ABC周長的取值范圍.
科目：高中數學 來源： 題型：
【題目】某中學為提升學生的英語學習能力，進行了主題分別為“聽”、“說”、“讀”、“寫”四場競賽．規定：每場競賽的前三名得分分別為
， 
， 
（
，且
， 
， 
），選手的最終得分為各場得分之和．最終甲、乙、丙三人包攬了每場競賽的前三名，在四場競賽中，已知甲最終分為
分，乙最終得分為
分，丙最終得分為
分，且乙在“聽”這場競賽中獲得了第一名，則“聽”這場競賽的第三名是（ ）
A. 甲 B. 乙 C. 丙 D. 甲和丙都有可能
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在發生某公共衛生事件期間，有專業機構認為該事件在一段時間沒有發生在規模群體感染的標志為“連續10天，每天新增疑似病例不超過7人”。根據過去10天甲、乙、丙、丁四地新增疑似病例數據，一定符合該標志的是 （ ）
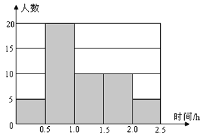
A. 甲地：總體均值為3，中位數為4
B. 乙地：總體均值為1，總體方差大于0
C. 丙地：中位數為2，眾數為3
D. 丁地：總體均值為2，總體方差為3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
， 
為兩條不同的直線， 
， 
為兩個不同的平面，對于下列四個命題：
①
， 
， 
， 
②
， 
③
， 
， 
④
， 
其中正確命題的個數有（ ）
A. 
個 B. 
個 C. 
個 D. 
個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=aln（x+1）+ 
x2﹣x，其中a為非零實數．
（1）討論函數f（x）的單調性；
（2）若y=f（x）有兩個極值點x1 ， x2 ， 且x1＜x2 ， 求證： 
＜ ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義數列
，如果存在常數
，使對任意正整數
，總有
，那么我們稱數列
為“
—擺動數列”．
（
）設
， 
， 
，判斷數列
， 
是否為“
—擺動數列”，并說明理由；
（2）已知“
—擺動數列”
滿足： 
，求常數
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有下列命題:
①函數
的圖象與
的圖象恰有
個公共點;
②函數
有
個零點;
③若函數
與
的圖像關于直線
對稱,則函數
與
的圖象也關于直線
對稱;
④函數
的圖象是由函數
的圖象水平向右平移一個單位后,將所得圖象在
軸右側部分沿
軸翻折到
軸左側替代
軸左側部分圖象,并保留右側部分而得到的.其中錯誤的命題有___________.（填寫所有錯誤的命題的序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）＝|x－1|＋|2x－1|．
（Ⅰ）若對 
x＞0，不等式f（x）≥tx恒成立，求實數t的最大值M；
（Ⅱ）在（Ⅰ）成立的條件下，正實數a，b滿足a2＋b2＝2M．證明：a＋b≥2ab．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
