【題目】已知函數
為奇函數．
（1）求a的值，并證明
是R上的增函數；
（2）若關于t的不等式f(t2－2t)＋f(2t2－k)＜0的解集非空，求實數k的取值范圍．
天天練口算系列答案科目：高中數學 來源： 題型：
【題目】設
，定義
（
，且
為常數），若
，
，
．以下四個命題中為真命題的是__________.
①
不存在極值；②若
的反函數為
，且函數
與函數
有兩個公共點，則
；③若
在
上是減函數，則實數的取值范圍是
；④若
，則在的曲線上存在兩點，使得過這兩點的切線互相垂直．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】《中華人民共和國道路交通安全法》第47條的相關規定：機動車行經人行橫道時，應當減速慢行；遇行人正在通過人行橫道，應當停車讓行，俗稱“禮讓斑馬線”，《中華人民共和國道路交通安全法》 第90條規定：對不禮讓行人的駕駛員處以扣3分，罰款50元的處罰.下表是某市一主干路口監控設備所抓拍的5個月內駕駛員不“禮讓斑馬線”行為統計數據：
月份 | 1 | 2 | 3 | 4 | 5 |
違章駕駛員人數 | 120 | 105 | 100 | 90 | 85 |
（1）請利用所給數據求違章人數
與月份之間的回歸直線方程
；
（2）交警從這5個月內通過該路口的駕駛員中隨機抽查了50人，調查駕駛員不“禮讓斑馬線”行為與駕齡的關系，得到如下
列聯表：能否據此判斷有
的把握認為“禮讓斑馬線”行為與駕齡有關？
不禮讓斑馬線 | 禮讓斑馬線 | 合計 | |
駕齡不超過1年 | 22 | 8 | 30 |
駕齡1年以上 | 8 | 12 | 20 |
合計 | 30 | 20 | 50 |
參考公式及數據：
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（其中
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，直線
與
相切于點
.
（1）求橢圓的方程；
（2）若直線
與橢圓交于不同的兩點
，
，與直線
相交于
（，，，均不重合）.證明：
為定值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我們知道一次函數、二次函數的圖像都是連續不斷的曲線，事實上，多項式函數的圖像都是如此.
（1）設
，且
，若還有
，求證：
；
（2）設一個多項式函數有奇次項
（
），求證：總能通過只調整的系數，使得調整后的多項式一定有零點；
（3）現有未知數為
的多項式方程
（其中實數
待定），甲、乙兩人進行一個游戲：由甲開始交替確定
中的一個數（每次只能去確定剩余還未定的數），當甲確定最后一個數后，若方程由實數解，則乙勝，反之甲勝，問：乙有必勝的策略嗎？若有，請給出策略并證明，若無，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市每年春節前后，由于大量的煙花炮竹的燃放，空氣污染較為嚴重．該市環保研究所對近年春節前后每天的空氣污染情況調查研究后發現，每天空氣污染的指數
隨時刻
(時)變化的規律滿足表達式
，
，其中
為空氣治理調節參數，且
．
（1）令
，求
的取值范圍；
（2）若規定每天中的最大值作為當天的空氣污染指數，要使該市每天的空氣污染指數不超過5，試求調節參數的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市舉行“中學生詩詞大賽”，分初賽和復賽兩個階段進行，規定：初賽成績大于90分的具有復賽資格．某校有800 名學生參加了初賽，所有學生的成績均在區間
內，其頻率分布直方圖如圖所示．
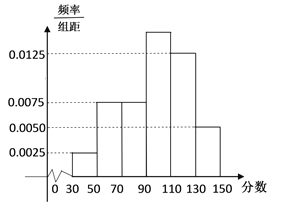
（Ⅰ）求初賽分數在區間
內的頻率；
（Ⅱ）求獲得復賽資格的人數；
（Ⅲ）據此直方圖估算學生初賽成績的平均數．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的中心在原點，離心率等于
，它的一個短軸端點恰好是拋物線
的焦點.
（1）求橢圓的方程；
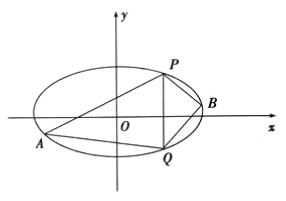
（2）已知
、
是橢圓上的兩點，
是橢圓上位于直線
兩側的動點.
①若直線
的斜率為，求四邊形
面積的最大值；
②當運動時，滿足
，試問直線的斜率是否為定值，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
， 
.
（1）若曲線
在
處的切線方程為
，求實數
的值；
（2）設
，若對任意兩個不等的正數
，都有
恒成立，求實數
的取值范圍；
（3）若在
上存在一點
，使得
成立，求實數
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
