
【題目】已知函數![]() ,
,![]() ,
,
(1)當![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)討論函數![]() 的單調性并判斷有無極值,有極值時求出極值.
的單調性并判斷有無極值,有極值時求出極值.
【答案】(1)![]() ;(2)見解析.
;(2)見解析.
【解析】試題分析:(1)欲求曲線![]() 在點
在點![]() 處的切線方程,只需求出斜率
處的切線方程,只需求出斜率![]() 和和
和和![]() 的值,即可利用直線的點斜式方程求解切線的方程;
的值,即可利用直線的點斜式方程求解切線的方程;
(2)求出![]() ,通過討論
,通過討論![]() 的取值范圍,求出函數的單調區間,從而求出函數的極值即可,可分
的取值范圍,求出函數的單調區間,從而求出函數的極值即可,可分![]() 兩種情況,求出函數的單調區間,得出函數的極值.
兩種情況,求出函數的單調區間,得出函數的極值.
試題解析:
(1)![]() 時,
時,![]() ,
,![]()
所以![]() ,
,![]()
因此曲線![]() 在點
在點![]() 處的切線方程是
處的切線方程是![]()
即![]()
(2)![]()
![]()
①當![]() 時,
時,![]() 恒成立,
恒成立,
所以當![]() 時
時![]() ,
,![]() 單調遞減
單調遞減
當![]() 時,
時,![]() ,
,![]() 單調遞增
單調遞增
所以當![]() 時,
時,![]() 取極小值
取極小值![]()
②當![]() 時,由
時,由![]() 得
得![]() 或
或![]()
(ⅰ)當![]() ,即
,即![]() 時
時
由![]() 得
得![]() 或
或![]()
由![]() 得
得![]()
所以![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,故
上單調遞增,故![]() 時,
時,![]() 取極大值
取極大值![]() ,
,![]() 時,
時,![]() 取極小值
取極小值![]()
(ⅱ)當![]() ,即
,即![]() 時,
時,![]() 恒成立
恒成立
此時函數![]() 在
在![]() 上單調遞增,函數
上單調遞增,函數![]() 無極值
無極值
(ⅲ)當![]() ,即
,即![]() 時
時
由![]() 得
得![]() 或
或![]()
由![]() 得
得![]()
所以![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,故
上單調遞增,故![]() 時,
時,![]() 取極大值
取極大值![]()
![]() 時,
時,![]() 取極小值
取極小值![]() .
.


 永乾教育寒假作業快樂假期延邊人民出版社系列答案
永乾教育寒假作業快樂假期延邊人民出版社系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為原點,極軸為
,以極點為原點,極軸為![]() 軸的正半軸建立平面直角坐標系,直線
軸的正半軸建立平面直角坐標系,直線![]() 的參數方程為
的參數方程為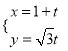 (
(![]() 為參數).
為參數).
(Ⅰ)寫出直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設曲線![]() 經過伸縮變換
經過伸縮變換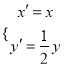 得到曲線
得到曲線![]() ,若點
,若點![]() ,直線
,直線![]() 與
與![]() 交與
交與![]() ,
, ![]() ,求
,求![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
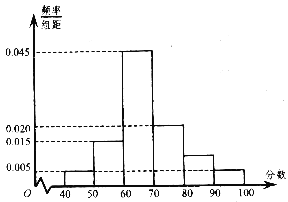
【題目】上周某校高三年級學生參加了數學測試,年部組織任課教師對這次考試進行成績分析.現從中隨機選取了40名學生的成績作為樣本,已知這40名學生的成績全部在40分至100分之間(滿分100分,成績不低于40分),現將成績按如下方式分成6組:第一組![]() ;第二組
;第二組![]() ;……;第六組
;……;第六組![]() ,并據此繪制了如圖所示的頻率分布直方圖.
,并據此繪制了如圖所示的頻率分布直方圖.
(Ⅰ)估計這次月考數學成績的平均分和眾數;
(Ⅱ)從成績大于等于80分的學生中隨機選2名,求至少有1名學生的成績在區間![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,現提供
,現提供![]() 的大致圖象的8個選項:
的大致圖象的8個選項:
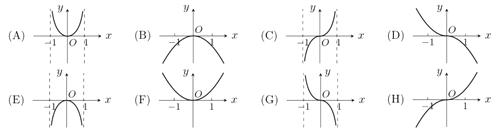
(1)請你作出選擇,你選的是( );
(2)對于函數圖像的判斷,往往只需了解函數的基本性質.為了驗證你的選擇的正確性,請你解決
下列問題:
①![]() 的定義域是___________________;
的定義域是___________________;
②就奇偶性而言, ![]() 是______________________ ;
是______________________ ;
③當![]() 時,
時, ![]() 的符號為正還是負?并證明你的結論.
的符號為正還是負?并證明你的結論.
(解決了上述三個問題,你要調整你的選項,還來得及.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】張師傅想要一個如圖1所示的鋼筋支架的組合體,來到一家鋼制品加工店定制,拿出自己畫的組合體三視圖(如圖2所示).店老板看了三視圖,報了最低價,張師傅覺得很便宜,當即甩下定金和三視圖,約定第二天提貨.第二天提貨時,店老板一臉壞笑的捧出如圖3–1所示的組合體,張師傅一看,臉都綠了:“奸商,怎能如此偷工減料”.店老板說,我是按你的三視圖做的,要不我給你加一個正方體,但要加價,隨機加上了一個正方體,得到如圖3–2所示的組合體;張師傅臉還是綠的,店老板又加上一個正方體,組成了如圖 3–3 所示的組合體,又加價;張師傅臉繼續綠,店老板再加一個正方體,組成如圖 3–4 所示的組合體,再次加價;雙方就三視圖爭吵不休……
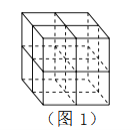
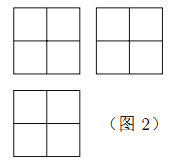
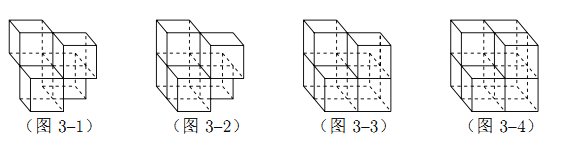
你認為店老板提供的![]() 個組合體的三視圖與張師傅畫的三視圖一致的個數是( )
個組合體的三視圖與張師傅畫的三視圖一致的個數是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位實行休年假制度三年以來,50名職工休年假的次數進行的調查統計結果如下表所示:
休假次數 | 0 | 1 | 2 | 3 |
人數 | 5 | 10 | 20 | 15 |
根據表中信息解答以下問題:
(1)從該單位任選兩名職工,求這兩人休年假次數之和為4的概率;
(2)從該單位任選兩名職工,用![]() 表示這兩人休年假次數之差的絕對值,求隨機變量
表示這兩人休年假次數之差的絕對值,求隨機變量![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,橢圓
,橢圓![]() 的離心率為
的離心率為![]() 是橢圓的焦點,直線
是橢圓的焦點,直線![]() 的斜率為
的斜率為![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的方程;
的方程;
(2)設過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,當
兩點,當![]() 的面積最大時,求直線
的面積最大時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ).
).
(1)若曲線![]() 在點
在點![]() 處的切線經過點
處的切線經過點![]() ,求
,求![]() 的值;
的值;
(2)若![]() 在區間
在區間![]() 上存在極值點,判斷該極值點是極大值點還是極小值點,并求
上存在極值點,判斷該極值點是極大值點還是極小值點,并求![]() 的取值范圍;
的取值范圍;
(3)若當![]() 時,
時, ![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com